Specyficzna składnia dialektów języka Lisp pozwala precyzyjnie określać i rozróżniać podstawowe konstrukcje, dodawać nowe elementy syntaktyczne, a nawet przekształcać kod programu w trakcie jego pracy. Wynika to z zastosowania prostych, jednak przemyślanych sposobów organizowania i reprezentowania kodu źródłowego.
Podstawowe konstrukcje
Programy pisane w odmianach języka Lisp charakteryzują się prostymi regułami składniowymi. Zamiast dyskutować o nich teoretycznie, rozpoczniemy praktycznym przykładem, na który będziemy się powoływać w celu poznania podstawowych mechanizmów rządzących tłumaczeniem kodu źródłowego na postać zrozumiałą dla komputera. Śledząc, co robi kompilator, lepiej zrozumiemy konstrukcje języka.
Oto nasz bazowy przykład:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
Nie jest specjalnie trudny. Prawda?
Składnia
Lisp z wyglądu przypomina owsiankę
z wmieszanymi obciętymi paznokciami.
— Larry Wall
Zacznijmy od składni (ang. syntax). Pierwszym, co rzuca się w oczy, gdy widzimy programy napisane w dialektach Lispu, jest umieszczanie niemal każdej złożonej konstrukcji w nawiasach. W innych językach programowania nawiasy służą do grupowania wybranych elementów składniowych, np. argumentów podczas wywoływania bądź definiowania funkcji, zestawu warunków czy działań na wartościach. W Lispach nawiasy są podstawowym elementem leksykalnym, używanym do nadawania kształtu całemu programowi i każdemu z wyrażeń.
W językach typu Lisp konstruujemy wyrażenia z zastosowaniem tzw. notacji polskiej (ang. Polish notation, skr. PN), zwanej też zapisem przedrostkowym (ang. prefix notation). Polega ona na tym, że najpierw umieszczamy operator (nazwę funkcji), a następnie operandy (argumenty wywołania). Nawiasów używamy, aby oznaczać początki i końce wyrażeń.
Notacja przedrostkowa jest różna od popularnego w wielu językach programowania zapisu wrostkowego (ang. infix), lecz nie na tyle, żeby wielce utrudniało to rozpoznawanie poszczególnych części wyrażeń. Nasz przykładowy program możemy w Rubym przedstawić tak:
print "Witaj, Lispie!"
print "Witaj, Lispie!"
A w języku C w następujący sposób:
#include <stdio.h>
int main(int argc, char *argv[]) {
printf("Witaj, Lispie!");
return 0;
}
#include <stdio.h>
int main(int argc, char *argv[]) {
printf("Witaj, Lispie!");
return 0;
}
Różnice między omawianymi rodzajami zapisu daje się dobrze zilustrować operacjami matematycznymi. Popatrzmy na dwa proste działania:
2 + 2 * 3
2 + 2 * 3
I zapis zgodny ze składnią języka Clojure:
(+ 2 (* 2 3))
(+ 2 (* 2 3))
Możemy zauważyć, że w drugim przykładzie operator dodawania i jego operandy są ujęte w nawiasy, a nazwa operacji znajduje się zawsze na pierwszej pozycji. Zaletą tego zapisu jest brak konieczności pamiętania o pierwszeństwie operatorów (ang. operator precedence).
Poza tym, aby w notacji polskiej reprezentować bardziej złożone konstrukcje, w których musimy wyrażać relacje przynależności, nie musimy korzystać z dodatkowych znaczników grupujących (takich jak np. nawiasy klamrowe lub wcięcia) czy separatorów (np. średników). Przetwarzanie składniowe wyrażeń w zapisie przedrostkowym jest prostsze i szybsze, ponieważ z racji wyraźniej określonej struktury wymaga mniejszej liczby reguł.
Czytnik
Wróćmy do naszego programu:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
Pierwszym etapem przekształcania jego tekstu do postaci wykonywalnej będzie wczytanie go do pamięci. W Lispach odpowiada za to komponent zwany czytnikiem (ang. reader). Jego zadanie polega na otwarciu pliku znajdującego się na dysku lub strumienia wejściowego skojarzonego z terminalem użytkownika i poddaniu wczytywanego tekstu przetwarzaniu, w którym wydzielić możemy dwie główne fazy:
-
związaną z wykrywaniem znanych konstrukcji leksykalnych w tekście;
-
związaną z wyodrębnianiem spośród znalezionych konstrukcji gramatycznie poprawnych wyrażeń i reprezentowaniem ich w postaci wewnętrznych, pamięciowych struktur.
Analiza leksykalna
Pierwsza faza wczytywania źródeł programu do pamięci to analiza leksykalna (ang. lexical analysis). Polega ona na:
-
oczyszczeniu wejścia ze zbędnych symboli;
-
rozpoznaniu w strumieniu znaków sekwencji pasujących do zdefiniowanych w leksykonie języka jednostek leksykalnych (ang. lexical units), w tym kontekście zwanych tokenami (ang. tokens);
-
wydzieleniu z tekstu fragmentów, które mają znaczenie składniowe (tzw. leksemów, ang. lexemes), będących swego rodzaju instancjami wykrytych tokenów.
Efektem analizy leksykalnej w odniesieniu do podanego przykładu będzie strumień leksemów, czyli wyodrębnionych fragmentów tekstu programu, które mają znaczenie składniowe:
| Leksem | Nazwa tokenu |
|---|---|
( |
literał listowy (otwierający) |
print |
symbol |
"Witaj, Lispie" |
literał łańcucha znakowego |
) |
literał listowy (zamykający) |
W opisanym procesie (zwanym tokenizacją) wydzielone leksemy mogą być opcjonalnie opatrywane informacjami o odpowiadających im tokenach, aby czynności tej nie trzeba było powtarzać podczas dalszych analiz.
Z powodu specyficznej składni języka Clojure (podobnie jak innych dialektów Lispu) analiza leksykalna jest w nim bardzo uproszczona i często sprowadza się do przekazania kontroli parserowi, gdy tylko znaleziony zostanie leksem.
Analiza składniowa
Drugą fazą przetwarzania kodu źródłowego do postaci przechowywanej w pamięci jest analiza składniowa (ang. syntactic analysis), nazywana też parsowaniem (ang. parsing). Obejmuje ona:
-
rozpoznanie w strumieniu leksemów konstrukcji składniowych (ang. syntactic constructs) przez porównanie ich rodzajów i umiejscowienia z regułami gramatycznymi języka;
-
wyodrębnienie wyrażeń (ang. expressions), czyli konstrukcji gramatycznych, które w późniejszych etapach kompilacji będzie można wartościować,
-
wytworzenie pamięciowych reprezentacji znalezionych wyrażeń z użyciem odpowiednich struktur danych;
-
umieszczenie powstałych obiektów w abstrakcyjnym drzewie składniowym (ang. abstract syntax tree, skr. AST).
Rezultatem analizy składniowej jest reprezentacja kodu źródłowego programu w pamięci dostępnej kompilatorowi.
Formy czytnika
Formy czytnika (ang. reader forms) to termin, którym w języku Clojure określamy jednostki leksykalne używane do tworzenia gramatycznie poprawnych konstrukcji składniowych.
Poniższa tabela zawiera podstawowe formy czytnika. W pierwszej kolumnie umieszczono nazwę tokenu, w drugiej przykłady leksemów, a w ostatniej typ danych obiektu w pamięci, który będzie reprezentował leksemy w abstrakcyjnym drzewie składniowym, jeżeli spełnione zostaną wymogi gramatyczne.
| Nazwa tokenu | Przykłady leksemów | Typ danych |
|---|---|---|
| symbol | razprzestrzeń/dwa |
Symbol |
| literał pusty | nil |
nil |
| literał kluczowy | :raz::dwa:przestrzeń/x::przestrzeń/y |
Keyword |
| literał łańcuchowy | "raz dwa" |
java.lang.String |
| literał listowy | (1 2 3) |
PersistentList |
| literał wektorowy | [1 2 3] |
PersistentVector |
| literał mapowy | {:a 1 :b 2}::{:a 1 :b2}:przestrzeń{:a 1 :b 2} |
PersistentArrayMapPersistentHashMap |
| literał logiczny | true, false |
java.lang.Boolean |
| literał liczby całkowitej | 10xff0172r1101 |
java.lang.Long |
| literał liczby wymiernej | 1/2 |
Ratio |
| literał liczby dużej | 1.2M1N |
java.math.BigDecimalBigint |
| literał liczby zmiennoprzecinkowej | -2.7e-4 |
java.lang.Double |
Makra czytnika
W Clojure część konstrukcji składniowych zrealizowana jest jako tzw. makra czytnika (ang. reader macros). Są to również podprogramy odpowiedzialne za przetwarzanie jednostek leksykalnych, jednak implementowane nieco inaczej. Zamiast być na sztywno wpisanymi w zestaw reguł czytnika, rezydują w specjalnej tabeli odczytu (ang. read table), gdzie określone tokeny są przypisane do podprogramów odpowiedzialnych za ich analizę.
W Clojure programista nie może modyfikować tabeli odczytu i nie wygląda na to, aby planowano dodać taką możliwość w przyszłości. Motywacją jest zachowanie ujednoliconej składni między projektami o różnym rodowodzie. Możemy jednak korzystać z tzw. literałów oznaczonych, które przypominają makra czytnika, chociaż podlegają pewnemu rygorowi syntaktycznemu.
Poniższa tabela przedstawia zestawienie makr czytnika:
| Nazwa tokena | Przykłady leksemów | Typ danych |
|---|---|---|
| cytowanie (ang. quote) | 'raz'(raz dwa) |
różne |
| cytowanie składniowe (ang. syntax-quote) |
`raz`(dwa trzy) |
różne |
| cofanie cytowania składniowego (ang. syntax unquote) |
~cytat |
różne |
| cofanie cytowania składniowego z rozplataniem (ang. syntax unquote-splicing) |
~@(list 1 2) |
różne |
| mapa metadanowa (ang. metadata map) |
^{:doc "Opis"} |
PersistentArrayMapPersistentHashMap |
| klucz metadanowy (ang. metadata key) |
^:dynamic true |
PersistentArrayMapPersistentHashMap |
| znacznik metadanowy (ang. metadata tag) |
^Integer x |
PersistentArrayMapPersistentHashMap |
| komentarz (ang. comment) |
; komentarz |
brak |
| literał znakowy (ang. character literal) |
\a, \b, \c, \newline |
java.lang.Character |
| wyrażenie dereferencyjne (ang. dereference expression) |
@x |
java.lang.Class (z IFn) |
| operator dostępu do składowej Javy (ang. Java member-access operator) |
(. " a " trim)(.trim " a ") |
różne |
| operator dostępu do składowych Javy (ang. Java member-access operators) |
(.. "a" trim length) |
różne |
| makro dyspozycyjne (ang. dispatch macro) | #… |
różne |
Ostatnia pozycja w tabeli to tzw. makro dyspozycyjne. Jest to ogólna nazwa
określająca podgrupę makr czytnika, których wszystkie tokeny rozpoczynają się
symbolem kratki (#). Gdy czytnik zauważa ten znak, przekazuje kontrolę nad dalszą
analizą konstrukcji do oddzielnej tablicy makr. Poniżej znajduje się lista tokenów,
których obsługa odbywa się z użyciem makra dyspozycyjnego:
| Nazwa tokena | Przykłady leksemów | Typ danych |
|---|---|---|
| cytowanie Varów (ang. var-quote) |
#'x |
Var |
| literał zbiorowy (ang. set literal) |
#{1 2 3} |
PersistentHashSet |
| wyrażenie regularne (ang. regular expression) |
#"raz.dw[aA]" |
java.util.regex.Pattern |
| literał funkcji anonimowej (ang. anonymous function literal) |
#(pr) |
java.lang.Class (z IFn) |
| argument funkcji anonimowej (ang. anonymous function argument) |
#(pr %)#(pr %1 %2) |
PersistentTreeMap |
| ignorowanie następnej formy (ang. ignore next form) |
#_ raz dwa |
brak |
| wywołanie konstruktora Javy (ang. Java constructor call) |
#nazwa.typ[:x]#nazwa.rekord{:x 1} |
różne |
| wyrażenie warunkowe czytnika (ang. reader conditional) |
$?(:clj "Clojure":cljs "ClojureScript") |
różne |
| literał oznaczony (ang. tagged literal) |
#symbol argument |
różne |
literał oznaczony inst(ang. inst tagged literal) |
#inst "2018-11-12" |
java.util.Date |
literał oznaczony UUID(ang. UUID tagged literal) |
#uuid "88b05082-392d-4e0a-89c9-cf62ec375c43" |
java.util.UUID |
Zauważmy, że niektóre jednostki leksykalne nie będą odzwierciedlane obiektami o z góry określonym typie danych (ze słowem „różne” w kolumnie typu). Na przykład cytowanie samo nie wiąże się z wytworzeniem konkretnej struktury, lecz wpływa na sposób dalszego parsowania danej konstrukcji. Znajdziemy też takie tokeny, które nie powodują wygenerowania żadnej wartości („brak” w kolumnie typu), ponieważ selektywnie wyłączą niektóre elementy tekstu programu z procesu analizy składniowej.
Na uwagę zasługuje również typ java.lang.Class z dopiskiem „z IFn”. Zapis ten
informuje o tym, że w Clojure obiekty funkcyjne wyrażane są przez anonimowe klasy
Javy wyposażone w interfejs IFn. Ma to związek z charakterystyką funkcji w Javie –
nie mają one takich właściwości, które pozwalałyby bezpośrednio z nich korzystać.
S-wyrażenia
Na poziomie gramatycznym każdy element kodu źródłowego w Lispie jest symbolicznie zapisanym wyrażeniem. Tekstowe reprezentacje wyrażeń – te, które widzimy w edytorze – to tzw. wyrażenia symboliczne (ang. symbolic expressions), nazywane skrótowo S-wyrażeniami (skr. S-expressions, sexprs, sexps).
Struktura S-wyrażeń przypomina trochę XML-a bądź JSON-a, tzn. mamy do czynienia z zapisem, który pozwala wyrażać zagnieżdżone i uporządkowane zestawy wartości, chociaż w nieco prostszy sposób niż wymienione formaty.
S-wyrażenie w Lispie możemy zdefiniować jako rodzaj notacji, w której:
- każdy element jest wyrażeniem:
- niezłożonym (zwanym atomem) lub
- składającym się z S-wyrażeń ujętych w nawiasy
i oddzielonych separatorem.
print ; atomowe S-wyrażenie (nie lista S-wyrażeń)
"Witaj, Lispie!" ; atomowe S-wyrażenie (nie lista S-wyrażeń)
(print "Witaj, Lispie!") ; listowe S-wyrażenie
() ; listowe i atomowe S-wyrażenie jednocześnie
(print (+ 2 2)) ; S-wyrażenie złożone z zagnieżdżonych S-wyrażeń
print ; atomowe S-wyrażenie (nie lista S-wyrażeń)
"Witaj, Lispie!" ; atomowe S-wyrażenie (nie lista S-wyrażeń)
(print "Witaj, Lispie!") ; listowe S-wyrażenie
() ; listowe i atomowe S-wyrażenie jednocześnie
(print (+ 2 2)) ; S-wyrażenie złożone z zagnieżdżonych S-wyrażeń
S-wyrażenie w Clojure będziemy definiowali w nieco bogatszy sposób, ponieważ mamy tam do czynienia z dodatkowymi literałami kolekcji. Będzie nim rodzaj notacji, w której:
- każdy element jest wyrażeniem:
- niezłożonym (zwanym atomem) lub
- składającym się z odseparowanych S-wyrażeń:
- w parach, ujętych w nawiasy klamrowe –
{…}; - w pojedynkę, ujętych w:
- nawiasy okrągłe –
(…); - klamry z symbolem kratki –
#{…}; - nawiasy kwadratowe –
[…].
- nawiasy okrągłe –
- w parach, ujętych w nawiasy klamrowe –
W przypadku wyrażeń w nawiasach klamrowych pierwsze elementy par muszą być unikatowymi wartościami w całym wyrażeniu, a w przypadku wyrażeń w nawiasach klamrowych z symbolem kratki każda wartość musi być unikatowa. Sprawdzanie wykonywane jest już podczas analizy składniowej, a gdy podany element wymaga wcześniejszego wyliczenia, podczas ewaluacji.
:raz ; atomowe S-wyrażenie
1 ; atomowe S-wyrażenie
print ; atomowe S-wyrażenie
"Witaj, Lispie!" ; atomowe S-wyrażenie
(print "Witaj, Lispie!") ; listowe S-wyrażenie
[1 2 3] ; wektorowe S-wyrażenie
#{1 2 3} ; zbiorowe S-wyrażenie
{:raz 1 :dwa 2 :trzy 3} ; mapowe S-wyrażenie
(str [1 2 3]) ; listowe i wektorowe S-wyrażenia
:raz ; atomowe S-wyrażenie
1 ; atomowe S-wyrażenie
print ; atomowe S-wyrażenie
"Witaj, Lispie!" ; atomowe S-wyrażenie
(print "Witaj, Lispie!") ; listowe S-wyrażenie
[1 2 3] ; wektorowe S-wyrażenie
#{1 2 3} ; zbiorowe S-wyrażenie
{:raz 1 :dwa 2 :trzy 3} ; mapowe S-wyrażenie
(str [1 2 3]) ; listowe i wektorowe S-wyrażenia
Rekurencyjna definicja S-wyrażenia może wydawać się mało zrozumiała, więc wspomożemy się naszym jednolinijkowym programem i dokonamy ręcznej kategoryzacji obecnych w nim elementów.
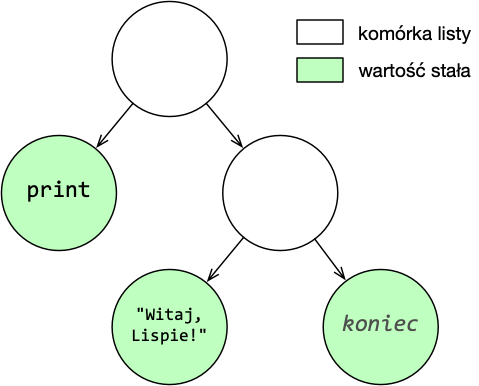
W zapisie (print "Witaj, Lispie!"):
(…)jest S-wyrażeniem, bo jest symbolicznie zapisaną listą S-wyrażeń;printjest S-wyrażeniem, bo jest atomem;"Witaj, Lispie!"jest S-wyrażeniem, bo jest atomem.
Graficznie można ten zestaw przedstawić w następujący sposób:
W odróżnieniu od innych Lispów złożone S-wyrażenia w Clojure budowane są nie tylko w oparciu o listy oznaczone nawiasami okrągłymi, ale również na bazie dodatkowych znaczników, które odpowiadają pewnym rodzajom kolekcji. Zależnie od użytego zapisu w pamięci powstanie struktura danych reprezentująca odpowiedni rodzaj S-wyrażenia:
| Notacja | Literał | S-wyrażenie | Struktura | Typ danych |
|---|---|---|---|---|
(a…z) |
listowy | listowe | lista | PersistentList |
[a…z] |
wektorowy | wektorowe | wektor | PersistentVector |
{a b … x y} |
mapowy | mapowe | mapa | PersistentArrayMapPersistentHashMap |
#{a…z} |
zbiorowy | zbiorowe | zbiór | PersistentHashSet |
Atomy
Omawiając symboliczne wyrażenia, wspomnieliśmy o ich specyficznej klasie zwanej atomami (ang. atoms). Atomem będzie taki element lispowej składni, który nie jest złożony (nie jest: listą, zbiorem, wektorem ani mapą). Wyjątki to pusta lista, pusty zbiór, pusty wektor i pusta mapa, które są zarówno wyrażeniami złożonymi, jak i atomami.
Do powyższej definicji należy jednak dodać jeszcze jeden istotny warunek, który decyduje o tym, że symboliczny zapis możemy uznać za lispowy atom. Przypomnijmy sobie nasz program:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
W poprzednich przykładach mogliśmy zauważyć, że print i Witaj, Lispie! są
atomami, ale czy byłyby nimi dowolne zestawy znaków, które nie są parą nawiasów
z zawartością? Nie. Atom musi być poprawną konstrukcją składniową, na podstawie
której czytnik będzie w stanie zdecydować, jaki obiekt umieścić w AST. Istnieje tu
więc pewien rygor. W tym konkretnym przypadku napis print zostanie zapamiętany
w postaci symbolu, a Witaj, Lispie! w formie łańcucha znakowego, ponieważ spełniają
składniowe warunki reprezentacji konkretnych struktur danych.
Owszem, reguły syntaktyczne są na tyle liberalne, że większość przypadkowo wpisanych słów czy nawet pojedynczych znaków zostanie uznanych za symbole (a więc atomy), jednak umieszczenie w symbolicznej etykiecie nawiasu czy rozpoczęcie jej cyfrą będą poważnymi nadużyciami i czytnik przestanie z nami współpracować.
Warto zaznaczyć, że pojęcie atomu jako klasy wyrażeń składniowych nie jest spopularyzowane w środowisku programistów języka Clojure. Wynika to prawdopodobnie z faktu, że w języku tym funkcjonuje referencyjny typ danych o nazwie Atom, który pomaga w przeprowadzaniu współbieżnych operacji na danych.
Listowe S-wyrażenia
Najczęściej spotykaną klasą S-wyrażeń są listowe S-wyrażenia (ang. list S-expressions). To właśnie dzięki nim programy pisane w dialektach języka Lisp składają się z dużej liczby nawiasów.
Listowe S-wyrażenie w Clojure powinno być listą elementów (innych S-wyrażeń), które oddzielone są znakami spacji, przecinka lub oboma tymi znakami. Początek i koniec listowego S-wyrażenia powinien być oznaczony otwierającym i zamykającym nawiasem okrągłym.
Listowe wyrażenia z umieszczonymi na pierwszych pozycjach symbolami służą do wywoływania podprogramów (funkcji, makr lub konstrukcji specjalnych) identyfikowanych z ich użyciem. Pozostałe elementy listy wyrażają wtedy argumenty przekazywane do wywołania. W przypadku funkcji wartości argumentów zostaną obliczone przed ich zaaplikowaniem.
Jeżeli nie podamy żadnych elementów, listowe S-wyrażenie spowoduje wygenerowanie pustej listy.
1;; wywołanie funkcji +
2(+ 1 2 3)
3;=> 6
4
5;; wywołanie makra defn
6;; służącego do definiowania funkcji nazwanej
7(defn powitaj [] "Witaj!")
8;=> #'user/powitaj
9
10;; wywołanie zdefiniowanej funkcji powitaj
11(powitaj)
12;=> "Witaj!"
13
14;; forma specjalna def
15;; służąca do definiowania zmiennej globalnej
16(def x 2)
17;=> #'user/x
18
19;; podwojenie wartości zmiennej globalnej
20;; identyfikowanej symbolem x
21(+ x x)
22;=> 4
23
24;; lista pusta
25()
26;=> ()
;; wywołanie funkcji +
(+ 1 2 3)
;=> 6
;; wywołanie makra defn
;; służącego do definiowania funkcji nazwanej
(defn powitaj [] "Witaj!")
;=> #'user/powitaj
;; wywołanie zdefiniowanej funkcji powitaj
(powitaj)
;=> "Witaj!"
;; forma specjalna def
;; służąca do definiowania zmiennej globalnej
(def x 2)
;=> #'user/x
;; podwojenie wartości zmiennej globalnej
;; identyfikowanej symbolem x
(+ x x)
;=> 4
;; lista pusta
()
;=> ()
Starsze dialekty Lispu obsługiwały nieco odmienną postać listowych S-wyrażeń. W parze
nawiasów nie umieszczano listy wszystkich elementów, ale tylko jedną jej komórkę
z podziałem na lewą i prawą wartość, które oddzielano znakiem kropki, a koniec listy
oznaczano symbolem nil, np.:
(+ . (1 . (2 . nil)))
(+ . (1 . (2 . nil)))
W Clojure ten rodzaj zapisu nie jest obsługiwany, chociaż istnieją struktury danych, które umożliwiają przeprowadzanie operacji na pojedynczych komórkach i tworzenie tzw. sekwencji.
Wektorowe S-wyrażenia
Literały wektorowe tworzą tzw. wektorowe S-wyrażenia, jednak w przeciwieństwie do wyrażeń listowych elementy umieszczane na ich pierwszych pozycjach nie mają specjalnego znaczenia. Efektem użycia wektorowego S-wyrażenia w podstawowej formie będzie struktura danych zwana wektorem, a każdy z elementów po uprzednim obliczeniu jego wartości stanie się jej składnikiem.
Z użyciem wektorowych S-wyrażeń możemy:
-
tworzyć wspomniane wyżej wektory i używać ich dla potrzeb logiki aplikacji,
-
określać listy argumentów definiowanych funkcji i makr,
-
wyrażać powiązania symboli z wartościami w odpowiednich konstrukcjach specjalnych (m.in.
letczybinding), -
dokonywać tzw. dekompozycji złożonych struktur o sekwencyjnym interfejsie dostępu.
;; wektor literalny
[1 2 3 4]
;=> [1 2 3 4]
;; wektor literalny
[(+ 1 1) 2 3 4]
;=> [1 2 3 4]
;; wektor powiązań w formie let
;; wytwarza leksykalne powiązanie symbolu a z wartością 1
(let [a 1] a)
;=> 1
;; wektorowa forma powiązaniowa w formie let (dekompozycja)
;; wewnątrz wektora powiązań formy let
;; dokonuje powiązania każdego symbolu z S-wyrażenia [a b]
;; z wartością inicjującą z S-wyrażenia [1 2]
;; zgodnie z pozycją występowania
(let [[a b] [1 2]]
(+ a b))
;=> 3
;; lista argumentów w definicji funkcji nazwanej
(defn dodaj
[a b]
(+ a b))
(dodaj 2 2)
;=> 4
;; wektor pusty
[]
;=> []
;; wektor literalny
[1 2 3 4]
;=> [1 2 3 4]
;; wektor literalny
[(+ 1 1) 2 3 4]
;=> [1 2 3 4]
;; wektor powiązań w formie let
;; wytwarza leksykalne powiązanie symbolu a z wartością 1
(let [a 1] a)
;=> 1
;; wektorowa forma powiązaniowa w formie let (dekompozycja)
;; wewnątrz wektora powiązań formy let
;; dokonuje powiązania każdego symbolu z S-wyrażenia [a b]
;; z wartością inicjującą z S-wyrażenia [1 2]
;; zgodnie z pozycją występowania
(let [[a b] [1 2]]
(+ a b))
;=> 3
;; lista argumentów w definicji funkcji nazwanej
(defn dodaj
[a b]
(+ a b))
(dodaj 2 2)
;=> 4
;; wektor pusty
[]
;=> []
Mapowe S-wyrażenia
Dzięki literałowi mapowemu możemy konstruować mapowe S-wyrażenia (ang. map S-expressions). W podstawowej formie pozwalają one wyrażać asocjacyjną strukturę danych zwaną mapą, która składa się ze zindeksowanych par typu klucz–wartość. Wartości powinny być oddzielone znakami spacji, znakami przecinka, albo obydwoma tymi znakami. Każdy pierwszy element w parze nazywamy kluczem (ang. key), a drugi wartością (ang. value).
Z użyciem mapowych S-wyrażeń możemy:
-
tworzyć wspomniane wyżej mapy i używać ich dla potrzeb logiki aplikacji,
-
określać listy argumentów nazwanych definiowanych funkcji i makr,
-
konstruować tzw. mapy metadanowe pozwalające wzbogacać niektóre konstrukcje w metadane, które mogą je opisywać bądź sterować ich właściwościami;
-
dokonywać dekompozycji złożonych struktur o asocjacyjnym interfejsie dostępu.
;; mapa literalna
{"a" 1 "b" 2}
;=> {"a" 1 "b" 2}
;; mapa wyrażająca argumenty nazwane
;; definiowanej funkcji
;; klucze a i b muszą być łańcuchami znakowymi
(defn dodaj [& {:strs [a b]}]
(+ a b))
;; wywołanie funkcji z argumentami nazwanymi
(dodaj "b" 1, "a" 3)
;=> 4
;; mapa metadanowa definiowanej funkcji
;; z łańcuchem dokumentującym (klucz :doc)
(defn dodaj
{:doc "Ta funkcja dodaje dwie liczby."}
[a b]
(+ a b))
;=> #'user/dodaj
;; wywołanie łańcucha dokumentującego dla dodaj
(doc dodaj)
;=>> -------------------------
;=>> user/dodaj
;=>> ([a b])
;=>> Ta funkcja dodaje dwie liczby.
;=> nil
;; mapowa forma powiązaniowa w formie let (dekompozycja)
;; wewnątrz wektora powiązań formy let
;; dokonuje powiązania symboli a i b
;; z wartościami pochodzącymi z mapy o indeksach "a" i "b"
(let [{:strs [a b]} {"b" 1 "a" 3}]
(+ a b))
;=> 4
;; mapa pusta
{}
;=> {}
;; mapa literalna
{"a" 1 "b" 2}
;=> {"a" 1 "b" 2}
;; mapa wyrażająca argumenty nazwane
;; definiowanej funkcji
;; klucze a i b muszą być łańcuchami znakowymi
(defn dodaj [& {:strs [a b]}]
(+ a b))
;; wywołanie funkcji z argumentami nazwanymi
(dodaj "b" 1, "a" 3)
;=> 4
;; mapa metadanowa definiowanej funkcji
;; z łańcuchem dokumentującym (klucz :doc)
(defn dodaj
{:doc "Ta funkcja dodaje dwie liczby."}
[a b]
(+ a b))
;=> #'user/dodaj
;; wywołanie łańcucha dokumentującego dla dodaj
(doc dodaj)
;=>> -------------------------
;=>> user/dodaj
;=>> ([a b])
;=>> Ta funkcja dodaje dwie liczby.
;=> nil
;; mapowa forma powiązaniowa w formie let (dekompozycja)
;; wewnątrz wektora powiązań formy let
;; dokonuje powiązania symboli a i b
;; z wartościami pochodzącymi z mapy o indeksach "a" i "b"
(let [{:strs [a b]} {"b" 1 "a" 3}]
(+ a b))
;=> 4
;; mapa pusta
{}
;=> {}
Zbiorowe S-wyrażenia
Literał zbiorowy umożliwia zapisywanie zbiorowych S-wyrażeń (ang. set S-expressions). Dzięki nim można w łatwy i przejrzysty sposób wyrażać zbiory, czyli struktury, w których każdy element występuje tylko raz.
Literał zbiorowy składa się z nawiasów klamrowych poprzedzonych znakiem kratki, wewnątrz których umieszczono niepowtarzalne w obrębie zbioru wartości. Elementy zbiorowego S-wyrażenia powinny być oddzielone znakiem spacji, przecinkiem lub obydwoma tymi znakami.
Jeżeli element wyrażenia zbiorowego nie jest wartością stałą, zostanie przeliczony zanim dojdzie do utworzenia obiektu reprezentującego zbiór.
#{1 2 3 4}
;=> #{1 2 3 4}
#{1 (+ 1 1) 3 4}
;=> #{1 2 3 4}
;; zbiór pusty
#{}
;=> #{}
#{1 2 3 4}
;=> #{1 2 3 4}
#{1 (+ 1 1) 3 4}
;=> #{1 2 3 4}
;; zbiór pusty
#{}
;=> #{}
Drzewo składniowe
Wiemy, że efektem analizy syntaktycznej jest forma kodu źródłowego w abstrakcyjnym drzewie składniowym. Spójrzmy, jak będzie ono wyglądało po wczytaniu naszego programu:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
Otwierający nawias na początku sprawi, że mechanizmy czytnika potraktują konstrukcję leksykalną jako literał listowy. Uwzględniając zawartość, będzie on tworzył gramatyczną konstrukcję: listowe S-wyrażenie. W fazie parsowania zostanie ono zmienione w obiekt listy, czyli struktury służącej do przechowywania uporządkowanego pod względem kolejności zestawu danych. Tymi danymi będą reprezentacje dwóch atomowych S-wyrażeń umieszczonych w nawiasach:

Drzewo składniowe nie jest elementem typowym dla Lispów. Korzystają z niego również kompilatory i interpretery innych języków programowania. Jednak w ich przypadku AST jest częściowo lub w całości niedostępne dla programisty i zbudowane w oparciu o wewnętrzne struktury danych, które nie są obsługiwane przez język. Operowanie na drzewie składniowym z poziomu programu jest tam niemożliwe lub ogranicza się do korzystania ze specjalnych mini-języków makrowych. W Lispach jest inaczej, o czym dowiemy się później.
Wracając do naszego programu… Pierwszym elementem listowego S-wyrażenia jest atom
print. Zostanie on rozpoznany jako kolejny znany element składni:
symbol. Reguły języka mówią, że musi on być wyrazem złożonym ze znaków
alfanumerycznych, który nie zaczyna się liczbą, ani znakiem specjalnym wskazującym na
daną innego rodzaju. W pamięciowej strukturze listy na pierwszej pozycji zostanie
więc umieszczony obiekt typu Symbol. Ten typ danych przypomina znane
z innych języków słowa kluczowe bądź etykiety tekstowe – będzie szerzej omówiony
w dalszej części.
Ostatni wprowadzony przez nas składnik symbolicznego wyrażenia to literał łańcucha
znakowego Witaj, Lispie!, który można wykryć po otaczających tekst
cudzysłowach. On również jest atomem i będzie potraktowany jako reprezentacja
łańcucha znakowego, który zostanie umieszczony na końcu listy rezydującej
w drzewie składniowym.
Podsumowując, w AST powstanie:
- struktura danych (lista) składająca się z:
- danej typu symbol,
- danej typu łańcuch znakowy.
Zauważmy, że graficzna reprezentacja kodu źródłowego w abstrakcyjnym drzewie składniowym i ukazana wcześniej forma organizowania S-wyrażeń są do siebie podobne. Przypadek?
Homoikoniczność
W Lispach pamięciowe obiekty AST są reprezentowane takimi samymi strukturami danych, z jakich możemy korzystać w programach. Co więcej, ich aranżacja w drzewie składniowym jest taka sama, jak układ S-wyrażeń w reprezentacji tekstowej. Innymi słowy: abstrakcyjne drzewo składniowe i tekst programu są izomorficzne. Gdyby zaszła konieczność, możemy wczytać AST i uzyskać czytelny kod źródłowy w postaci wyrażeń symbolicznych.
Opisana tu cecha zwana jest jednoznacznością lub homoikonicznością (ang. homoiconicity) i otwiera możliwość transformowania S-wyrażeń odwzorowanych w AST z użyciem systemu makr składniowych, któremu poświęcony będzie osobny rozdział.
Semantyka
Kolejnym ważnym etapem przekształcania programu do postaci wykonywalnej jest analiza semantyczna (ang. semantic analysis), czyli proces rozpoznawania konstrukcji znaczeniowych języka. W dialektach Lispu jest to jedno z pierwszych zadań komponentu zwanego ewaluatorem (ang. evaluator). Polega ono na odczytywaniu obiektów abstrakcyjnego drzewa składniowego reprezentujących wyrażenia, sprawdzaniu czy są one znaczeniowo poprawne i obliczaniu wartości każdego z nich przez uruchamianie odpowiednich podprogramów. W przypadku Clojure część tego procesu zostanie zrealizowana podczas kompilacji, a część w trakcie uruchamiania programu.
Przywołajmy raz jeszcze nasz przykład:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
Po wczytaniu kodu źródłowego do pamięci w AST znalazły się reprezentujące go dane, a w toku pracy programu będzie przeprowadzane wartościowanie każdej z nich, aby finalnie uzyskać wartość najbardziej zewnętrznego S-wyrażenia.
W podanym przykładzie pierwszym elementem listy jest symbol print, który
identyfikuje wbudowaną funkcję języka Clojure służącą do wyświetlania tekstu na
ekranie. Badając bieżącą przestrzeń nazw kompilator znajdzie odpowiednie
odwzorowanie symbolu na funkcyjny obiekt i ustali, że ma
do czynienia z konstrukcją, która jest wywołaniem funkcji. Poza tym zidentyfikuje
podprogram, który należy wywołać, aby wykonać operację.
Funkcje mogą przyjmować argumenty, a podane wyrażenie symboliczne zawiera również
(poza nazwą operacji) przeznaczony dla jej wywołania argument. Ponieważ w Lispach
mamy do czynienia z przekazywaniem przez wartość, zostanie najpierw przeprowadzony
proces wartościowania łańcucha Witaj, Lispie!. Łańcuch znakowy jest wartością
stałą, więc nie będzie wymagane dalsze przeliczanie, a do wywołania przekazana
zostanie właśnie ona.
Uruchomienie podprogramu funkcji print sprawi, że powstanie zamierzony efekt
uboczny w postaci wyświetlenia na ekranie napisu:
Witaj, Lispie!
Dodatkowo funkcja zwróci wartość, która zależnie od sposobu uruchomienia programu będzie wyświetlona (w przypadku interaktywnej konsoli) lub pozostanie nieobsłużona (w innych przypadkach).
Formy
Abstrakcyjne drzewo składniowe w Lispach to dane (ang. data) zorganizowane w postaci zagnieżdżonych list. Każda taka dana (ang. datum) jest lispową formą (ang. lisp form), nazywaną skrótowo formą (ang. form), czyli pamięciową reprezentacją poprawnego składniowo S-wyrażenia przeznaczonego do wartościowania.
Ewaluator, analizując elementy AST, próbuje obliczać ich wartości, zwracając uwagę na typy danych i konteksty ich występowania. Możliwych jest kilka głównych ścieżek decyzyjnych podprogramu wartościującego, które będą się przekładać na różne rodzaje znalezionych form.
Badając wyłącznie struktury danych w AST czy S-wyrażenia w tekście kodu źródłowego,
nie możemy precyzyjnie określić z jaką konkretnie formą będziemy mieć
do czynienia. Można to ustalić dopiero podczas ewaluacji. Na przykład symbol x
umieszczony na pierwszym miejscu listowego S-wyrażenia (x 1) może po wartościowaniu
zmienić się w obiekt funkcyjny i wtedy będzie to forma wywołania funkcji x, ale
może też okazać się na przykład mapą, a wtedy będzie to forma przeszukiwania mapy,
gdzie wartość 1 traktowana jest jak klucz.
Zanim przejdziemy do omawiania głównych rodzajów form, nazwijmy te, które zostaną rozpoznane w naszym programie:
(print "Witaj, Lispie!")
(print "Witaj, Lispie!")
(…)– forma złożona,print– forma symbolowa,"Witaj, Lispie!"– forma normalna,(print "Witaj, Lispie!")– forma wywołania funkcji:- po wykryciu, że
printpowiązano z funkcją; - po wykryciu formy argumentów funkcji;
- po przeliczeniu argumentu do formy normalnej.
- po wykryciu, że
Formy stałe i normalne
Wyrażenie kodu źródłowego reprezentujące stałą wartość, która nie wymaga przeliczania, zostanie przez ewaluator rozpoznane jako tzw. forma stała (ang. constant form) i przekazane bez zmian do wywołującej, nadrzędnej konstrukcji.
Najbardziej bezpośrednim rodzajem formy stałej jest tzw. forma normalna (ang. normal form), czyli taka dana kodu źródłowego, która z natury nie wymaga wartościowania, ponieważ już w drzewie składniowym jest reprezentowana wartością własną. Przykładem będą tu m.in. literały liczbowe i literały łańcuchów znakowych.
"Witaj, Lispie!" ; łańcuch tekstowy
\a ; znak
() ; lista pusta
123 ; liczba całkowita
'lalala ; zacytowany symbol
"Witaj, Lispie!" ; łańcuch tekstowy
\a ; znak
() ; lista pusta
123 ; liczba całkowita
'lalala ; zacytowany symbol
Ciekawym rodzajem formy stałej będzie rezultat zastosowania formy cytowania
(ang. quote form) – specjalnej formy składniowej, która umożliwia wyłączanie
wartościowania przekazywanych jej S-wyrażeń i potraktowanie danych kodu źródłowego
jak stałych struktur. Konstrukcja quote i mechanizm cytowania zostaną dokładniej
omówione w dalszej części.
Formy symbolowe
Symbol będzie przez ewaluator potraktowany jak forma symbolowa (ang. symbol form) i spróbuje on odnaleźć powiązany z nim obiekt, który – zależnie od kontekstu – może być przyporządkowany do nazwy tego symbolu w różnych miejscach, np. w powiązaniach leksykalnych bądź przestrzeniach nazw (i zmiennych globalnych). Uzyskana wartość zostanie podstawiona w miejsce występowania symbolu.
print
+
print
+
Zobacz także:
- „Formy symbolowe”, rozdział IV.
Formy złożone
Gdy ewaluator napotka niepustą kolekcję, rozpozna ją jako tzw. formę złożoną (ang. compound form).
W przypadku formy mapowej (ang. map form), formy wektorowej (ang. vector form) lub formy zbiorowej (ang. set form) przeprowadzone będzie wartościowanie każdego z elementów i zwrócona zostanie kolekcja, której każdy element jest przeliczony do formy stałej.
[1 2 3] ; forma wektorowa
#{1 2 3} ; forma zbiorowa
{"a" 1 "b" 2} ; forma mapowa
'(1 2 3) ; forma listowa (lista literalna)
[1 2 3] ; forma wektorowa
#{1 2 3} ; forma zbiorowa
{"a" 1 "b" 2} ; forma mapowa
'(1 2 3) ; forma listowa (lista literalna)
W przypadku listy lub sekwencji obiektów typu Cons zostanie obliczona
wartość pierwszego elementu i zapadnie decyzja odnośnie dalszej ścieżki postępowania
w zależności od wykrytej formy.
Formy przeszukiwania
Jeżeli pierwszym elementem wartościowanej formy listowej będzie wektor, zbiór lub mapa, rozpoznana zostanie odpowiednio: forma przeszukiwania wektora (ang. vector lookup form), forma przeszukiwania zbioru (ang. set lookup form) bądź forma przeszukiwania mapy (ang. map lookup form). Wartość następnego elementu listy zostanie przekazana jako argument do podprogramu odpowiadającego za odnajdywanie elementów o podanych indeksach. Jeżeli argumentów będzie więcej, wygenerowany zostanie błąd.
([1 2 3] 0) ;=> 1
(#{1 2 3} 2) ;=> 2
({"a" 1 "b" 2} "b") ;=> 2
([1 2 3] 0) ;=> 1
(#{1 2 3} 2) ;=> 2
({"a" 1 "b" 2} "b") ;=> 2
Jeżeli pierwszym elementem wartościowanej formy listowej będzie słowo kluczowe lub symbol literalny, rozpoznana zostanie kluczowa forma przeszukiwania (ang. keyword lookup form) bądź symbolowa forma przeszukiwania (ang. symbol lookup form), a wartość kolejnego elementu listy będzie przekazana jako argument wywołania podprogramu, który użyje podanego klucza bądź symbolu jako indeksu w celu odszukania wartości. Jeżeli argumentów będzie więcej, wygenerowany zostanie błąd.
(:a {:a 1 :b 2}) ;=> 1
(:a #{:a :b :c}) ;=> :a
('a {'a 1 'b 2 :c 3}) ;=> 1
(:a {:a 1 :b 2}) ;=> 1
(:a #{:a :b :c}) ;=> :a
('a {'a 1 'b 2 :c 3}) ;=> 1
Formy wywołania funkcji
Jeżeli pierwszym elementem wartościowanej formy listowej będzie obiekt funkcyjny, wyrażenie zostanie potraktowane jako forma wywołania funkcji (ang. function-call form), zaś przeliczone wartości pozostałych elementów listy zostaną przekazane jako argumenty wywołania podprogramu skojarzonego z tym obiektem. Dotyczy to również metod Javy.
(print "Witaj, Lispie!") ;=> nil =>> Witaj, Lispie!
(+ 2 2) ;=> 4
(.toLowerCase "A") ;=> a
(print "Witaj, Lispie!") ;=> nil =>> Witaj, Lispie!
(+ 2 2) ;=> 4
(.toLowerCase "A") ;=> a
Formy specjalne
Jeżeli pierwszym elementem wartościowanej formy listowej będzie jedna z tzw. form składniowych (ang. syntax forms), uruchomiony zostanie wbudowany podprogram obsługi skojarzonej z nią formy specjalnej (ang. special form), a pozostałe elementy listy staną się jego argumentami (po ich uprzednim wartościowaniu lub bez wartościowania).
(def x 1) ; definiowanie zmiennej globalnej
(fn [x] (inc x)) ; tworzenie funkcji
(def f (fn [x] (inc x))) ; definiowanie funkcji nazwanej
(let [a 1] a) ; tworzenie powiązań leksykalnych
(quote (1 2 3)) ; cytowanie
(. System (getProperty "user.home")) ; dostęp do klas Javy
(def x 1) ; definiowanie zmiennej globalnej
(fn [x] (inc x)) ; tworzenie funkcji
(def f (fn [x] (inc x))) ; definiowanie funkcji nazwanej
(let [a 1] a) ; tworzenie powiązań leksykalnych
(quote (1 2 3)) ; cytowanie
(. System (getProperty "user.home")) ; dostęp do klas Javy
Formy specjalne są – jak sama nazwa mówi – formami, które cechują specjalne zasady wartościowania. W istocie forma specjalna to rodzaj wbudowanej w język funkcji, której – podobnie jak w przypadku makr – nie wszystkie argumenty od razu są przeliczane.
Dzięki formom specjalnym możemy na przykład definiować zmienne globalne czy funkcje, a także tworzyć powiązania symboli z wartościami w pewnych obszarach programu.
Rekurencyjne wartościowanie form
Gdy uzyskana w toku pracy ewaluatora dana okaże się nie być wartością stałą, lecz
kolejną formą wymagającą wartościowania, zostanie rekurencyjnie przeliczona, aż
do uzyskania formy stałej. Na przykład forma symbolowa może wyemanować z siebie
obiekt referencyjny Var, który z kolei będzie wskazywał na podprogram
wywoływanej funkcji.
Niepoprawne formy
Jeżeli okaże się, że dany element AST nie jest poprawną formą, to znaczy taką, której wartości nie można obliczyć (zredukować do formy stałej), wygenerowany zostanie komunikat o błędzie, a program awaryjnie zakończy pracę.
1(1 2 3) ; liczby 1 nie można rzutować na typ funkcyjny
2(()) ; listy pustej nie można rzutować na typ funkcyjny
3(+ /) ; funkcji / nie można rzutować na liczbę całkowitą
4(nie_ma) ; brak konstrukcji identyfikowanej symbolem nie_ma
5nie_ma ; brak konstrukcji identyfikowanej symbolem nie_ma
(1 2 3) ; liczby 1 nie można rzutować na typ funkcyjny
(()) ; listy pustej nie można rzutować na typ funkcyjny
(+ /) ; funkcji / nie można rzutować na liczbę całkowitą
(nie_ma) ; brak konstrukcji identyfikowanej symbolem nie_ma
nie_ma ; brak konstrukcji identyfikowanej symbolem nie_ma
Nazwy niektórych form są umowne, tzn. bazują na założeniu, że pewne S-wyrażenia dadzą się przeliczyć do danych konkretnych typów. Na przykład zapis:
(dodaj 1 2 3)
(dodaj 1 2 3)
nazwiemy umownie formą wywołania funkcji, chociaż w istocie nie mamy pewności, czy
forma symbolowa dodaj będzie rozpoznana w przestrzeni nazw jako zmienna globalna,
a znajdujący się tam obiekt referencyjny będzie zawierał odniesienie do funkcji.
Formy powiązaniowe
Forma powiązaniowa (ang. binding form) to konstrukcja, w której do symbolicznego identyfikatora przypisywana jest wartość, aby wytworzyć powiązanie. Na poziomie składniowym będziemy w tych formach mieli do czynienia z niezacytowanymi symbolami, jednak nie będą one traktowane jak formy symbolowe, których wartości należy poznać, lecz właśnie jako wyrażenia przypisujące pamięciowe obiekty do symbolicznych nazw.
Formę powiązaniową rozpoznamy w wyrażeniach reprezentujących pewne formy specjalne, gdzie będziemy mieli do czynienia z:
-
parą złożoną z niezacytowanego symbolu i innej formy (reprezentującej wartość, która po obliczeniu ma być przypisana);
-
niezacytowanego symbolu występującego samodzielnie, np. w wektorze parametrycznym funkcji, gdzie wartość będzie dynamicznie przypisana podczas przekazywania argumentów przy jej wywołaniu.
Formy powiązaniowe symboli są składnikiem niektórych form złożonych i specjalnych. Znajdziemy je na przykład:
-
w argumencie określającym nazwę:
-
- formy specjalnej
leti podobnych, - formy specjalnej
loopi podobnych, - makra
with-local-vars, - makra
binding;
- formy specjalnej
-
w argumencie określającym nazwę i/lub wektorze parametrycznym:
Dodatkowo formy powiązaniowe mogą pojawić się również w tzw. powiązaniach strukturalnych, czyli abstrakcyjnych powiązaniach, w których dochodzi do dekompozycji złożonych struktur danych i przypisania symbolom wartości na wskazanych pozycjach lub identyfikowanych podanymi kluczami. Będziemy mieli wtedy do czynienia z powiązaniową formą wektora (ang. vector binding form) lub powiązaniową formą mapy (ang. map binding form), w której zamiast pojedynczego, niezacytowanego symbolu po lewej stronie pojawia się wektorowe bądź mapowe S-wyrażenie.
Niektóre inne konstrukcje korzystające z form powiązaniowych możemy również
intuicyjnie określać mianem form powiązaniowych. Będą to takie wyrażenia, których
celem jest przede wszystkim wykształcanie powiązań. Na przykład formę
specjalną let nazwiemy też formą powiązaniową let (ang. let binding form),
mimo że w istocie korzysta ona z potencjalnie wielu podstawowych form powiązaniowych
zgrupowanych w wektorze powiązań.
(def x 5) ; symbol x w formie powiązaniowej
(fn [x] nil) ; symbol x formie powiązaniowej
(let [x 2]) ; symbol x w formie powiązaniowej
(defn nazwa ; symbol nazwa w formie powiązaniowej (nazwa funkcji)
[x] ; symbol x w formie powiązaniowej (nazwa parametru)
nil)
(def x 5) ; symbol x w formie powiązaniowej
(fn [x] nil) ; symbol x formie powiązaniowej
(let [x 2]) ; symbol x w formie powiązaniowej
(defn nazwa ; symbol nazwa w formie powiązaniowej (nazwa funkcji)
[x] ; symbol x w formie powiązaniowej (nazwa parametru)
nil)
Warto zauważyć, że w przypadku argumentów funkcji symbole identyfikujące ich parametry będą dynamicznie przypisywane do wartości przekazywanych argumentów w momentach wywołania funkcji.
Zobacz także:
- „Powiązania”;
- „Formy powiązaniowe symboli”, rozdział IV;
- „Powiązania i przestrzenie nazw”, rozdział VI.
Cytowanie
Ważną konstrukcją specjalną w Clojure i innych Lispach jest forma specjalna quote,
która pozwala wyłączać wartościowanie S-wyrażenia podanego jako jej
argument. Zapisana w ten sposób konstrukcja składniowa zostanie wczytana
i przeanalizowana syntaktycznie, jednak faza analizy znaczeniowej będzie dla niej
pominięta. W AST znajdą się odpowiednie struktury danych, jednak będą oznaczone jako
formy stałe. Zamiast obliczać ich wartości, ewaluator po prostu zwróci struktury
danych znalezione w drzewie składniowym.
W dialektach Lispu użycie formy quote pozwala stwarzać literalne warianty
struktur, które w postaciach niezacytowanych byłyby użyte do reprezentowania kodu
źródłowego programu i/lub wartościowane.
quote
1(quote raz) ; literalny symbol
2(quote (1 2 3)) ; literalna lista
3(quote [a b]) ; literalny wektor
4(quote {a 1 b 2}) ; literalna mapa
5(quote #{1 2 3}) ; literalny zbiór
(quote raz) ; literalny symbol
(quote (1 2 3)) ; literalna lista
(quote [a b]) ; literalny wektor
(quote {a 1 b 2}) ; literalna mapa
(quote #{1 2 3}) ; literalny zbiór
Powyższe można zapisać także posługując się lukrem składniowym:
'raz
'(1 2 3)
'[a b]
'{a 1 b 2}
'#{a b}
Te same struktury danych moglibyśmy wytworzyć nie stosując cytowania, ale korzystając z odpowiednich, wbudowanych funkcji języka:
1(symbol "raz") ; symbol
2(list 1 2 3) ; lista
3(vector (symbol "a") (symbol "b")) ; wektor
4(hash-map (symbol "a") 1 (symbol "b" 2}) ; mapa
5(hash-set 1 2 3) ; zbiór
(symbol "raz") ; symbol
(list 1 2 3) ; lista
(vector (symbol "a") (symbol "b")) ; wektor
(hash-map (symbol "a") 1 (symbol "b" 2}) ; mapa
(hash-set 1 2 3) ; zbiór
Cytowanie jest rekurencyjne, tzn. każde S-wyrażenie zagnieżdżone w cytowanym również będzie zacytowane.
1(quote (a b c)) ; lista z literalnymi symbolami
2(quote (+ 2 (* 2 3))) ; lista z literalnymi symbolami i liczbami
3(quote [raz 2 3]) ; wektor z literalnym symbolem i liczbami
4(quote {a 1 b 2}) ; mapa z literalnymi symbolami i liczbami
5(quote #{a b c}) ; zbiór z literalnymi symbolami
(quote (a b c)) ; lista z literalnymi symbolami
(quote (+ 2 (* 2 3))) ; lista z literalnymi symbolami i liczbami
(quote [raz 2 3]) ; wektor z literalnym symbolem i liczbami
(quote {a 1 b 2}) ; mapa z literalnymi symbolami i liczbami
(quote #{a b c}) ; zbiór z literalnymi symbolami
Warto zauważyć, że terminy „literalna mapa”, „literalny zbiór” i „literalny wektor” mogą być w pewnych kontekstach uznane za określenia użyte nadgorliwie. Każdy z elementów symbolicznie wyrażonych map, zbiorów czy wektorów zostanie zachłannie obliczony przez ewaluator i na tym ich wartościowanie się zakończy. Nadal pozostaną takimi samymi strukturami danych i nie niosą takiego ładunku składniowego jak listy.
Uzupełnianie nazw wymienionych wyżej struktur o określenie „literalny” bądź „literalna” będzie miało sens wtedy, gdy zechcemy zaznaczyć, że zawartości ich elementów nie będą obliczane. Przykładem może być sytuacja, w której elementami wektorowego S-wyrażenia są symbole wskazujące na pewne wartości. Gdy taką konstrukcję zacytujemy, nie dojdzie do przeliczania wartości elementów podczas wartościowania wektora. Jeżeli chcemy ten fakt podkreślić, możemy nazwać wektor literalnym.
[1 2 3] ; forma wektorowa (pot. wektor, rzadko: literalny wektor)
[1 2 (inc 2)] ; forma wektorowa (pot. wektor)
'[1 2 (inc 2)] ; literalny wektor (pot. wektor)
'[1 2] ; literalny wektor
[1 2 3] ; forma wektorowa (pot. wektor, rzadko: literalny wektor)
[1 2 (inc 2)] ; forma wektorowa (pot. wektor)
'[1 2 (inc 2)] ; literalny wektor (pot. wektor)
'[1 2] ; literalny wektor
Najrozsądniejszym wydaje się określać mapy, wektory i zbiory jako literalne wtedy, gdy są wyrażane w sposób zacytowany. W przypadku postaci niezacytowanych (podlegających wartościowaniu) można korzystać z potocznych określeń.
Spróbujmy jeszcze zastosować cytowanie w odniesieniu do naszego szablonowego programu:
'(print "Witaj, Lispie!")
'(print "Witaj, Lispie!")
Efekt wartościowania powyższego wyrażenia to wartość, którą jest lista zawierająca symbol i łańcuch znakowy, czyli nasz pierwotny program, dający wyrazić się tekstem:
(print "Witaj, Lispie!")
Warto zauważyć, że gdy zacytowana zostanie forma stała, jej wartością po
przeliczeniu będzie wciąż jej poprzednia, stała wartość, co możemy zaobserwować
w przypadku łańcucha znakowego Witaj, Lispie!.
Identyfikatory
Identyfikatory (ang. identifiers) to konstrukcje, które pozwalają nazywać tożsamości (np. pojedyncze wartości czy złożone struktury danych umieszczane w pamięci), aby można się było do nich potem odwoływać.
W Clojure istnieją konstrukcje identyfikacyjne (omawiane niżej symbole), które mają specjalne znaczenie składniowe i nazywane przez nie obiekty są rozpoznawane automatycznie. Znajdziemy też takie (np. klucze), które posłużą nam do identyfikacji danych użytkowych, ale nie ma obowiązku ich używać.
Symbole
Symbol (ang. symbol) w Clojure to typ danych (ang. data type), którego instancje służą do identyfikowania umieszczonych w pamięci struktur. Dzięki symbolom (i odpowiedniemu ich traktowaniu przez mechanizmy czytnika) możemy nadawać nazwy funkcjom oraz ich argumentom, rezultatom obliczeń i innym obiektom, a następnie odwoływać się do nich z użyciem czytelnych identyfikatorów.
W Clojure formy symbolowe można wyrażać w tekście programu bez stosowania żadnych dodatkowych oznaczeń. Nazwa symbolu jest jednocześnie jego własnym identyfikatorem, chociaż obiekt symbolu umieszczony w AST będzie podlegał dalszemu przeliczaniu przez ewaluator (nie będzie wartością własną).
Składniowo rzecz ujmując, każdy symbol ma nazwę, która musi być łańcuchem znakowym
rozpoczynającym się znakiem niebędącym cyfrą i mogącym zawierać znaki alfanumeryczne
oraz: *, +, !, -, _ i ?.
1funk ; funk to forma symbolowa
2(funk 1 2 3) ; funk to forma symbolowa w formie wywołania funkcji
3(fn [x y] x) ; symbole x oraz y są parametrami anonimowej funkcji
4 ; [x y] zawiera dwie formy powiązaniowe symboli
5(.toLowerCase "A") ; toLowerCase jest metodą klasy Javy
6
7; ChunkedSeq to klasa wewnętrzna klasy PersistentVector
8(new clojure.lang.PersistentVector$ChunkedSeq [1 2 3 4 5] 0 3)
funk ; funk to forma symbolowa
(funk 1 2 3) ; funk to forma symbolowa w formie wywołania funkcji
(fn [x y] x) ; symbole x oraz y są parametrami anonimowej funkcji
; [x y] zawiera dwie formy powiązaniowe symboli
(.toLowerCase "A") ; toLowerCase jest metodą klasy Javy
; ChunkedSeq to klasa wewnętrzna klasy PersistentVector
(new clojure.lang.PersistentVector$ChunkedSeq [1 2 3 4 5] 0 3)
W wielu Lispach symbol jest typem referencyjnym, to znaczy samodzielnie identyfikuje inny obiekt, przechowując odwołanie do jego pamięciowej struktury. W przypadku Clojure jest inaczej – symbol nie zawiera żadnego odwołania, a to, że używając symbolowych form można wywoływać funkcje bądź odnosić się do stałych wartości zawdzięczamy odpowiedniemu traktowaniu przez ewaluator i przeszukiwaniu dodatkowych struktur (np. przestrzeni nazw czy obszaru powiązań leksykalnych).
Specjalne znaczenie ma umieszczony wewnątrz tekstowej nazwy symbolu znak kropki
(.), który pozwala budować identyfikatory odnoszące się do nazw klas
(ang. class names) systemu gospodarza, czyli Javy.
Symbole z przestrzeniami
Symbol może opcjonalnie zawierać dodatkową nazwę określającą tzw. przestrzeń nazw, czyli specjalny zbiór, który służy do grupowania identyfikatorów w celu eliminowania konfliktów. Więcej szczegółów o korzystaniu z tego mechanizmu sterowania widocznością można znaleźć w dalszej części tego odcinka.
Nazwa przestrzeni jest łańcuchem znakowym podlegającym takiemu samemu rygorowi
syntaktycznemu, jak nazwa symbolu, a wyrażamy ją przez umieszczenie przed nazwą
symbolu i oddzielenie znakiem ukośnika (/), na przykład:
1my/funk ; symbol funk z przestrzenią my
2(my/funk 1 2) ; symbol funk z przestrzenią my w formie wywołania funkcji
my/funk ; symbol funk z przestrzenią my
(my/funk 1 2) ; symbol funk z przestrzenią my w formie wywołania funkcji
W obiekcie symbolu nie znajdziemy innego niż tekstowe odwołania do przestrzeni. Tu również nie dochodzi do przechowywania referencji. Możemy podać nieistniejącą przestrzeń i nie będzie to błąd, dopóki ewaluator nie zacznie wartościować zapisu.
Symbole literalne
Symbole znajdziemy przede wszystkim w abstrakcyjnym drzewie składniowym, tzn. będą formami symbolowymi, które reprezentują identyfikatory innych obiektów. Dodatkowo możemy korzystać z symboli literalnych (form stałych) w logice aplikacji. Będą wtedy na przykład pełniły funkcję prostych typów wyliczeniowych (ang. enumerated types), reprezentując stałe wartości wchodzące w skład ustalonych zbiorów:
1(list (symbol "trochę") (symbol "bardzo") (symbol "najbardziej"))
2(list 'trochę 'bardzo 'najbardziej)
3'(trochę bardzo najbardziej)
(list (symbol "trochę") (symbol "bardzo") (symbol "najbardziej"))
(list 'trochę 'bardzo 'najbardziej)
'(trochę bardzo najbardziej)
Powyższe trzy zapisy są równoważne. Pierwszy konstruuje literalną listę, której
elementami są symbole tworzone na bazie łańcuchów znakowych z użyciem wbudowanej
funkcji symbol; drugi również spowoduje powstanie listy, ale do wyrażania
literalnych symboli korzystamy z cytowania; trzeci natomiast czyni użytek
z rekurencyjnego cytowania całego listowego S-wyrażenia.
Formy stałe symboli mogą też zawierać określenie przestrzeni nazw:
(symbol "nazwa" "przestrzeń")
'nazwa/przestrzeń
Czasami w Lispach używa się literalnych symboli jako kluczy indeksujących w strukturach asocjacyjnych (np. mapach):
{ 'trochę 21, 'bardzo 108, 'najbardziej 11 }
{ 'trochę 21, 'bardzo 108, 'najbardziej 11 }
W Clojure nie zaleca się używania symboli w tym celu z uwagi na fakt, że nie są internalizowane, tzn. dwa symbole o takiej samej nazwie będą reprezentowane przez dwa różne pamięciowe obiekty. Innymi słowy: w Clojure instancje symboli o takich samych nazwach nie są singletonem.
Gdybyśmy w programie wykorzystali symbole do indeksowania obszernych struktur o częstym dostępie, powstawałoby bardzo wiele tymczasowych obiektów, z którymi musiałby sobie radzić mechanizm odśmiecania pamięci, poświęcając cenny czas. Kolejny minus to mniej wydajne porównywanie wartości (a więc i przeszukiwanie), ponieważ zestawiane ze sobą byłyby nazwy symboli, a nie wewnętrzne identyfikatory obiektów.
Zobacz także:
- „Symbole”, rozdział IV.
Klucze
Słowo kluczowe (ang. keyword), zwane potocznie kluczem (ang. key) to typ
danych, który – podobnie jak symbole – służy do identyfikowania innych
obiektów, jednak w Clojure nie ma specjalnego znaczenia składniowego i klucze nie
identyfikują automatycznie innych konstruktów programu. Klucze wyrażane są obiektami
typu clojure.lang.Keyword.
W przeciwieństwie do symboli klucze są internalizowane. Dwa słowa kluczowe o tej samej nazwie będą w pamięci reprezentowane przez ten sam obiekt (ich singleton).
Słowa kluczowe sprawdzają się w roli prostych typów wyliczeniowych lub indeksów w asocjacyjnych strukturach danych (np. mapach). Jeżeli chodzi o wbudowane mechanizmy języka Clojure, ze słowami kluczowymi spotkamy się m.in. w niektórych makrach i konstrukcjach wyrażających powiązania argumentów nazwanych funkcji.
Ze składniowego punktu widzeni każdy klucz ma nazwę, która musi być łańcuchem znakowym
rozpoczynającym się dwukropkiem (:) i mogącym zawierać znaki alfanumeryczne oraz:
*, +, !, -, _ i ?. W praktyce możemy korzystać z nieco bogatszego zestawu
znaków (np. coraz częstsze jest wykorzystywanie kropki dla oznaczenia wewnętrznych
hierarchii w niektórych bibliotekach), jednak może to ulec zmianie w przyszłości,
dlatego warto używać nazw kluczy zgodnych z dokumentacją języka.
Klucze są również funkcjami. Gdy umieścimy słowo kluczowe na pierwszym miejscu listowego S-wyrażenia, wywołany zostanie podprogram, który spróbuje odszukać indeks w asocjacyjnej lub zbiorowej kolekcji podanej jako argument.
Podobnie jak symbole, klucze mogą opcjonalnie zawierać określenie przestrzeni nazw.
:klucz ; klucz
::klucz ; klucz z bieżącą przestrzenią nazw
:przestrzeń/klucz ; klucz z przestrzenią
::user/klucz ; klucz z przestrzenią (istniejącą)
(keyword "klucz") ; klucz z łańcucha znakowego
(keyword "przestrzeń" "klucz") ; jw. lecz z określeniem przestrzeni
{:a 1 :b 2} ; mapa z indeksami w postaci kluczy
(defn x [& {:keys [kolor]}] kolor) ; funkcja z argumentem nazwanym, kluczowym
(x :kolor 123) ; wywołanie funkcji z argumentem kluczowym
(:a {:a 1 :b 2}) ; klucz jako funkcja przeszukująca mapę
(:a #{:a :b :c :d}) ; klucz jako funkcja przeszukująca zbiór
:klucz ; klucz
::klucz ; klucz z bieżącą przestrzenią nazw
:przestrzeń/klucz ; klucz z przestrzenią
::user/klucz ; klucz z przestrzenią (istniejącą)
(keyword "klucz") ; klucz z łańcucha znakowego
(keyword "przestrzeń" "klucz") ; jw. lecz z określeniem przestrzeni
{:a 1 :b 2} ; mapa z indeksami w postaci kluczy
(defn x [& {:keys [kolor]}] kolor) ; funkcja z argumentem nazwanym, kluczowym
(x :kolor 123) ; wywołanie funkcji z argumentem kluczowym
(:a {:a 1 :b 2}) ; klucz jako funkcja przeszukująca mapę
(:a #{:a :b :c :d}) ; klucz jako funkcja przeszukująca zbiór
Zobacz także:
- „Klucze”, rozdział IV.
Przestrzenie nazw
W języku Clojure korzysta się z konstruktu zwanego przestrzenią nazw (ang. namespace). W technologii informacyjnej terminem tym określa się mechanizm sterowania widocznością identyfikatorów, który pozwala na ich hierarchiczne grupowanie w celu unikania konfliktów. Popularnymi przykładami przestrzeni nazw mogą być struktury katalogowe systemów plikowych, rekordy DNS czy publiczne adresy IP.
Przestrzenie nazw w programowaniu komputerów pomagają oddzielać od siebie zbiory identyfikatorów używane w różnych komponentach (np. bibliotekach programistycznych) lub kontekstach, dzięki czemu udostępniane nazwy (np. modułów, klas, zmiennych czy funkcji) są unikatowe. Możemy wtedy korzystać w programie z kilku bibliotek, w których zdefiniowano tak samo nazwaną funkcję. Podczas odwoływania się do niej wymagane będzie użycie tzw. nazwy w pełni kwalifikowanej (ang. fully qualified name), zwanej też nazwą jednoznaczną, czyli identyfikatora wzbogaconego o określenie nazwy przestrzeni.
W Clojure przestrzenie nazw zrealizowane są jako globalnie widoczne mapy, czyli
słowniki przechowujące odwzorowania typu klucz–wartość. W ich przypadku kluczami są
symbole, a wartościami zmienne globalne lub klasy Javy. Typ danych
używany do reprezentowania obiektów przestrzeni to clojure.lang.Namespace.
Ponieważ umieszczane w programie symbole mogą opcjonalnie zawierać określenie
przestrzeni nazw, więc możliwe jest z ich użyciem odwoływanie się do identyfikatorów
z różnych przestrzeni. Jeżeli symbol nie zawiera nazwy jednoznacznej, wtedy podczas jego
wartościowania przyjmuje się, że identyfikuje on konstrukcję zdefiniowaną w aktualnej
przestrzeni, wskazywanej przez dynamiczną zmienną globalną
clojure.core/*ns*:
;; symbol select z przestrzeni clojure.set
;; identyfikuje funkcję
(clojure.set/select odd? #{1 2 3 4})
;=> #{1 3}
;; symbol + z przestrzeni clojure.core
;; zaimportowanej do bieżącej (user)
;; identyfikuje funkcję
(+ 2 2)
;=> 4
;; symbol select z przestrzeni clojure.set
;; identyfikuje funkcję
(clojure.set/select odd? #{1 2 3 4})
;=> #{1 3}
;; symbol + z przestrzeni clojure.core
;; zaimportowanej do bieżącej (user)
;; identyfikuje funkcję
(+ 2 2)
;=> 4
Pierwszy symbol w powyższym przykładzie ma nazwę select i przestrzeń nazw określoną
łańcuchem znakowym clojure.set. Ponieważ jest to forma wywołania funkcji, będzie
potraktowany jak identyfikator funkcji, której podprogram trzeba uruchomić. Aby
odnaleźć funkcyjny obiekt, przeszukana zostanie przestrzeń nazw clojure.set,
a w niej odnaleziony zostanie klucz identyfikowany symbolem select i przypisana do
niego zmienna globalna. Wewnątrz obiektu referencyjnego
znalezione będzie odniesienie do podprogramu funkcji, który zostanie wywołany
z argumentami podanymi jako kolejne elementy listowego S-wyrażenia (odd? oraz #{1 2 3 4}).
Drugi symbol z przykładu nie ma określonej przestrzeni nazw. Ewaluator odczyta więc
zawartość globalnej zmiennej dynamicznej *ns*, która domyślnie w konsoli REPL
wskazuje na przestrzeń user. W niej znajdzie powiązanie symbolu + ze obiektem
Var, który odnosi się do wbudowanej funkcji sumującej. Ta ostatnia
oryginalnie nie rezyduje w przestrzeni nazw user, lecz została do niej
zaimportowana wraz z innymi odwzorowaniami z przestrzeni clojure.core podczas
uruchamiania konsoli.
Zobacz także:
- „Powiązania i przestrzenie nazw”, rozdział VI.
Obsługa globalnych stanów
Opowiadając o Clojure, podkreśla się, że nie ma tam konwencjonalnych zmiennych, a struktury danych są niemutowalne. Dlaczego więc raz po raz przewija się określenie „zmienna globalna”?
Każdy język programowania musi radzić sobie z wyrażaniem zmieniających się, globalnych stanów, czyli ulegających zmianom wartości, które widoczne są w całym programie pod stałymi nazwami. Przykładami mogą być: kondycja postaci w grze, układ okien interfejsu użytkownika bądź aktualnie przetwarzana zawartość wczytywanego pliku.
Do reprezentowania opisanych wyżej danych można by użyć konwencjonalnych zmiennych, czyli ustalonych przestrzeni pamięciowych o określonych nazwach, których zawartości są modyfikowane przez odpowiednie podprogramy (np. zmieniający punktację, reagujący na działania użytkownika odnośnie elementów interfejsu czy odczytujący dane z bazy). Jednak w takim modelu nie będziemy mogli posłużyć się wieloma wątkami bez stosowania dodatkowych mechanizmów izolacji. Pamięciowa szufladka zmiennej, reprezentująca ważny parametr, może zostać zreorganizowana przez jeden wątek, podczas gdy drugi będzie jeszcze przeprowadzał z jej użyciem ważną operację. Oznacza to więcej pracy dla programisty, który zamiast skupiać się na logice biznesowej aplikacji, musi pamiętać o zabezpieczaniu programu przed nim samym i wprowadzać semafory, blokady itp.
Podejście przeciwne do wyżej opisanego polega na rezygnacji z współdzielonych stanów, czyli model czysto funkcyjny, w którym nie można modyfikować żadnych już użytych obszarów pamięci, zaś cały program składa się z operacji, których jedynym wejściem są argumenty, a jedynym wyjściem zwracane wartości. Obsługa interfejsów graficznych czy śledzenie aktywności zalogowanego użytkownika byłyby w takim układzie kłopotliwe w wyrażaniu i mało wydajne. Wyobraźmy sobie, że każda czynność użytkownika uruchamia kaskadę wywołań funkcji, które za każdym razem od początku wyliczają wartości wszystkich parametrów składających się na stan całego programu w danym momencie.
W Clojure mamy do czynienia z rozsądnym kompromisem. Nie istnieją co prawda konwencjonalne zmienne, lecz dzięki odpowiednim typom referencyjnym (ang. reference types) jesteśmy w stanie śledzić i obsługiwać zmieniające się globalne stany. Oznacza to, że mutacje danych są dopuszczalne, ale tylko na zasadzie wyjątku i tylko z użyciem specjalnych konstrukcji.
Obiekty referencyjne w Clojure wyposażono w bezpieczne pod względem wykonywania współbieżnego mechanizmy aktualizowania i odczytu wskazywanych przez nie wartości bieżących. Zamiast bezpośredniego modyfikowania obszaru pamięci zawierającego dane, dochodzi więc do aktualizacji odwołania w taki sposób, że obiekt zaczyna wskazywać na nową wartość (umieszczoną w innym miejscu). Wartości pozostają więc stałe i nie muszą rezydować w zmiennych, ponieważ jedynym elementem ulegającym mutacji (nadpisaniu przestrzeni w pamięci) są odwołania do nich rezydujące w obiektach referencyjnych.
Typ Var
Najpowszechniej wykorzystywanym typem referencyjnym w Clojure jest
Var. Pozwala on tworzyć odwołania do umieszczanych w pamięci danych
i dokonywać zmian tych odwołań w obrębie danego wątku wykonywania. Dodatkowo
obiekt typu Var może opcjonalnie zawierać tzw. odwołanie główne, które będzie
współdzielone między wszystkimi wątkami i używane w przypadku braku odwołania
ustawionego w konkretnym.
Zwyczajowo obiekty typu Var są w Clojure internalizowane w przestrzeniach nazw,
tzn. nie istnieje powszechnie używana forma specjalna czy funkcja, która pozwalałaby
tworzyć je bez powiązania z jakimiś symbolicznymi identyfikatorami. Jest jednak makro
with-local-vars, które tworzy obiekty Var w zasięgu leksykalnym – muszą być one
wtedy identyfikowane podanymi symbolami widocznymi w wyrażeniu podanym jako
argument. Wskazywane w ten sposób wartości możemy odczytywać z użyciem funkcji
deref lub literału dereferencyjnego (umieszczanego przed symbolem znaku małpki):
(with-local-vars [a 5] @a)
;=> 5
(with-local-vars [a 5] @a)
;=> 5
Zobacz także:
- „Typ Var”, rozdział VII.
Zmienne globalne
Obiekty typu Var (a dokładniej clojure.lang.Var) są wraz z symbolami
wykorzystywane w Clojure do tworzenia zmiennych globalnych (ang. global
variables). Zmienne globalne służą do identyfikowania rzadko zmieniających się
tożsamości, np. wartości konfiguracyjnych czy zdefiniowanych w programie
funkcji.
Działa to tak, że konkretny Var zostaje przyporządkowany do symbolicznej nazwy
przez umieszczenie wpisu w jednej z przestrzeni nazw. Powstaje wtedy
globalne powiązanie symbolu z wartością bieżącą obiektu
typu Var.
Spójrzmy na diagram ilustrujący sposób uzyskiwania obiektu funkcyjnego na podstawie jego nazwy w naszym przykładowym programie:
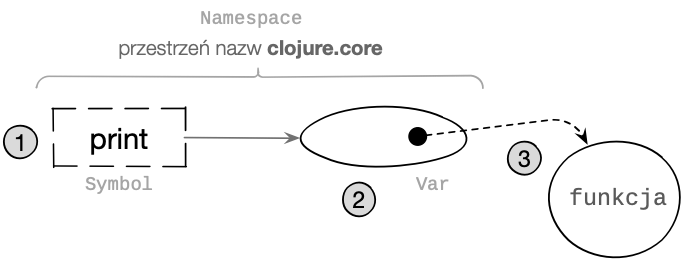
Ewaluator wykonał tu 3 istotne kroki w celu uzyskania podprogramu wywoływanej funkcji:
-
Przeszukał przestrzeń nazw
clojure.corew celu odnalezienia wartości przypisanej do symboluprint. -
Uzyskał obiekt typu
Vari przekazał go do odpowiedniego podprogramu, aby odczytać wartość bieżącą referencji. -
Znalazł wskazywany zmienną referencyjną obiekt funkcyjny, którego podprogram można wywołać.
Tworzenie zmiennych globalnych możliwe jest z użyciem formy specjalnej def:
1(def x 8) ; x wskazuje na wartość 8
2(def y [1 2 3]) ; y wskazuje na wektor [1 2 3]
3(def pisz print) ; pisz wskazuje na wartość bieżącą zmiennej print
4(declare potem) ; tworzy zmienną globalną bez powiązania z wartością
5
6(pisz x) ;=> 8
7(pisz y) ;=> [1 2 3]
8(pisz "Witaj, Lispie!") ;=> Witaj, Lispie!
9
10potem
11;=> #object[clojure.lang.Var$Unbound 0x53245a5b "Unbound: #'user/potem"]
(def x 8) ; x wskazuje na wartość 8
(def y [1 2 3]) ; y wskazuje na wektor [1 2 3]
(def pisz print) ; pisz wskazuje na wartość bieżącą zmiennej print
(declare potem) ; tworzy zmienną globalną bez powiązania z wartością
(pisz x) ;=> 8
(pisz y) ;=> [1 2 3]
(pisz "Witaj, Lispie!") ;=> Witaj, Lispie!
potem
;=> #object[clojure.lang.Var$Unbound 0x53245a5b "Unbound: #'user/potem"]
Zobacz także:
- „Powiązania i przestrzenie nazw”, rozdział VI;
- „Zmienne globalne”, rozdział VI.
Powiązania
Powiązanie (ang. binding) to w ujęciu ogólnym skojarzenie identyfikatora z identyfikowanym obiektem. Używając tego terminu, unikamy nieporozumień związanych z subtelnymi, ale istotnymi z punktu widzenia programisty różnicami w odwoływaniu się do obiektów z użyciem nazw.
W językach zakorzenionych imperatywnie często korzystamy z pojęcia „zmienna” i siłą nawyku oczekujemy, że będzie ona miała jakąś nazwę. Termin ten pozwala nam wskazać pamięciową szufladkę, w której znajdziemy wartość. W Clojure takie podejście mogłoby wprowadzać w błąd, ponieważ możemy stwarzać zmienne pozbawione nazw (obiekty referencyjne), a także nazywać wartości, które wcale zmiennymi nie są.
W języku Clojure mamy do czynienia z kilkoma rodzajami powiązań:
-
Zmienne globalne to powiązania:
- symboli z obiektami typu
Varw przestrzeniach nazw, - symboli z klasami Javy w przestrzeniach nazw.
- symboli z obiektami typu
-
Powiązania leksykalne to powiązania symboli z wartościami w wektorze powiązań formy specjalnej
let. -
Wektory parametryczne to formy powiązaniowe symboli z przyjmowanymi argumentami w definicjach funkcji i makr .
-
Powiązania strukturalne to abstrakcyjne powiązania:
- symboli z wartościami na wskazanych pozycjach kolekcji sekwencyjnych,
- symboli z wartościami identyfikowanymi kluczami kolekcji asocjacyjnych.
-
Obiekty typów referencyjnych to powiązania obiektów z wskazywanymi przez nie wartościami bieżącymi.
Ostatnia pozycja wymaga wyjaśnienia, ponieważ – jak łatwo zauważyć – nie zawiera wzmianki o żadnym symbolu, a wielokrotnie przecież wspominaliśmy, że to właśnie symbole służą do identyfikowania innych obiektów.
W tym miejscu warto sobie przypomnieć, że w Clojure symbole samodzielnie nie
przechowują odwołań do wartości – tę funkcję pełnią obiekty referencyjne (np. typu
Var w przypadku zmiennych globalnych). Wynika to z przyjętego modelu
zarządzania zmiennym stanem.
;; zmienna globalna
;; wartość początkowa wskazywana przez x to 1
(def x 1)
;=> #'user/x
;; wektor parametryczny definicji funkcji
;; dwa pierwsze argumenty staną się parametrami a i b
(fn [a b] (+ a b))
;=> #<Fn@5af25442 user/eval14406[fn]>
;; powiązanie leksykalne
;; symbol a identyfikuje wartość 1
(let [a 1]
a)
;=> 1
;; dekompozycja pozycyjna w let
;; symbol a powiązany z wartością 1 przez pozycję
;; symbol b powiązany z wartością 2 przez pozycję
(let [[a b] '(1 2 8)]
(+ a b))
;=> 3
;; dekompozycja asocjacyjna w let
;; symbol a powiązany z wartością 1 przez klucz :a
;; symbol b powiązany z wartością 2 przez klucz :b
(let [{a :a b :b} {:a 1 :b 2 :c 8}]
(+ a b))
;=> 3
;; dekompozycja asocjacyjna w let (użycie :keys)
;; symbol a powiązany z wartością 1 przez klucz :a
;; symbol b powiązany z wartością 2 przez klucz :b
(let [{:keys [:a :b]} {:a 1 :b 2 :c 8}]
(+ a b))
;=> 3
;; powiązanie obiektu referencyjnego typu Var z wartością
(with-local-vars [x 5] x)
;=> #'Var: --unnamed-->
;; powiązanie obiektu referencyjnego typu Atom z wartością
(atom 5)
;=> #<Atom@a1cb453 5>
;; zmienna globalna
;; wartość początkowa wskazywana przez x to 1
(def x 1)
;=> #'user/x
;; wektor parametryczny definicji funkcji
;; dwa pierwsze argumenty staną się parametrami a i b
(fn [a b] (+ a b))
;=> #<Fn@5af25442 user/eval14406[fn]>
;; powiązanie leksykalne
;; symbol a identyfikuje wartość 1
(let [a 1]
a)
;=> 1
;; dekompozycja pozycyjna w let
;; symbol a powiązany z wartością 1 przez pozycję
;; symbol b powiązany z wartością 2 przez pozycję
(let [[a b] '(1 2 8)]
(+ a b))
;=> 3
;; dekompozycja asocjacyjna w let
;; symbol a powiązany z wartością 1 przez klucz :a
;; symbol b powiązany z wartością 2 przez klucz :b
(let [{a :a b :b} {:a 1 :b 2 :c 8}]
(+ a b))
;=> 3
;; dekompozycja asocjacyjna w let (użycie :keys)
;; symbol a powiązany z wartością 1 przez klucz :a
;; symbol b powiązany z wartością 2 przez klucz :b
(let [{:keys [:a :b]} {:a 1 :b 2 :c 8}]
(+ a b))
;=> 3
;; powiązanie obiektu referencyjnego typu Var z wartością
(with-local-vars [x 5] x)
;=> #'Var: --unnamed-->
;; powiązanie obiektu referencyjnego typu Atom z wartością
(atom 5)
;=> #<Atom@a1cb453 5>
Zobacz także:
- „Powiązania i przestrzenie nazw”, rozdział VI.
Kolekcje
Kolekcja (ang. collection) to struktura danych, która pozwala przechowywać pewną liczbę elementów.
Listy
W Lispie najczęściej używaną strukturą danych jest lista, która – jak mieliśmy okazję zauważyć – służy zarówno do składniowej organizacji kodu programu (listowe S-wyrażenia), jak i do przechowywania uporządkowanej kolekcji elementów dla potrzeb logiki aplikacji. Warto wyobrażać sobie listę jako sposób aranżacji danych, a nie tylko symboliczny zapis z nawiasami.
Istnieje kilka rodzajów list. Najczęściej używane w dialektach Lispu to tzw. listy połączone (ang. linked lists), a dokładniej listy jednokierunkowe (ang. singly linked lists). Cechuje je możliwość elastycznego łączenia ze sobą elementów i szybkiego dodawania nowych do ich początków. Właśnie dlatego dobrze spełniają swe zadanie jako pamięciowe reprezentacje struktur lispowych programów.
Listy we wczesnych Lispach
Historycznie rzecz ujmując, każdy węzeł listy (w Lispie nazywany komórką cons, ang. cons cell) ma dwa sloty: pierwszy wskazuje na wartość bieżącego elementu, a drugi na kolejny element listy (kolejną komórkę cons). Tak naprawdę są to po prostu dwa wskaźniki, które mogą odnosić się do dowolnych wartości.
Dostęp do pierwszego slotu każdego z elementów nazywamy car (z ang. Contents
of the Address part of Register number), a do drugiego cdr (z ang. Contents
of the Decrement part of Register number). Etymologia tych dziwnych nazw pochodzi
z czasów, gdy implementowano Lispa na komputerze IBM 704 (lata
pięćdziesiąte). Maszyna ta miała specjalną instrukcję, która dzieliła 36-bitowe słowo
maszynowe na 4 części – car i cdr to skrócone etykiety dwóch pierwszych,
a w Lispie znalazły się dlatego, że autor używał ich do dzielenia zawartości
wewnętrznej struktury reprezentującej komórkę listy. Żargonowo pierwszy slot komórki
cons określa się więc skrótem CAR, a drugi CDR.
Nic nie stoi na przeszkodzie, aby lista zawierała w sobie inną listę:
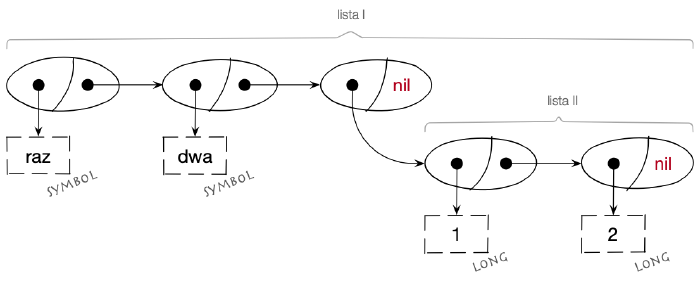
W kodzie możemy wyrazić powyższą strukturę jako:
(raz dwa (1 2))
(raz dwa (1 2))
czyli:
1(raz ; pierwszy element listy
2 dwa ; drugi element listy
3 ( ; trzeci element listy – lista zagnieżdżona
4 1 ; pierwszy element zagnieżdżonej listy
5 2)) ; drugi element zagnieżdżonej listy
(raz ; pierwszy element listy
dwa ; drugi element listy
( ; trzeci element listy – lista zagnieżdżona
1 ; pierwszy element zagnieżdżonej listy
2)) ; drugi element zagnieżdżonej listy
A tak wyglądałby zapis z użyciem tzw. notacji pełnej, która w Clojure nie jest używana. W każdej parze nawiasów znajdziemy dwa sloty oddzielone znakiem kropki:
(raz . (dwa . ((1 . (2 . nil)) . nil)))
(raz . (dwa . ((1 . (2 . nil)) . nil)))
Kropki oddzielają tu rejestry komórek CAR i CDR, a elementy nil oznaczają końce
list. Jeżeli drugi slot (CDR) ma wskazywać na kolejny element listy, w zapisie ten
drugi jest umieszczany po kropce i ujmowany w nawiasy.
Pamiętajmy jednak, że zapis (raz dwa (1 2)) jest poprawnym S-wyrażeniem, ale nie
jest formą, chyba że zdefiniujemy funkcję nazwaną raz, a symbol dwa skojarzymy
z jakąś wartością. Możemy też użyć cytowania i odebrać konstrukcji
specjalne znaczenie, aby wyrażała formę stałą:
'(raz dwa (1 2))
'(raz dwa (1 2))
W pierwszych wydaniach języka Lisp listy tworzyło się z użyciem funkcji cons
(z ang. construct, pol. konstruować). Na przykład:
(cons 'raz (cons 'dwa (cons (cons 1 (cons 2 nil)) nil)))
(cons 'raz (cons 'dwa (cons (cons 1 (cons 2 nil)) nil)))
Co można przedstawić też jako:
(cons 'raz
(cons 'dwa
(cons (cons 1
(cons 2 nil))
nil)))
Takie budowanie list może i gimnastykuje umysł, jednak nie służy produktywnemu
pisaniu programów. Obecnie niektóre z dialektów Lispu zrezygnowały z obsługi notacji
pełnej, chociaż funkcji cons nadal się używa, ale raczej
do przeprowadzania operacji na istniejących listach, niż do ich konstruowania od
zera.
Listy w Clojure
W języku Clojure listy reprezentowane są obiektowym typem danych systemu gospodarza
o nazwie clojure.lang.PersistentList. Obiekty tego typu znajdziemy w drzewie
składniowym, gdzie odzwierciedlą listowe S-wyrażenia, a także w danych aplikacji, gdy
użyto funkcji list lub wytworzono literalną listę przez
zacytowanie jej symbolicznie wyrażonej postaci.
1(list 1 2 3) ; użycie funkcji list (argumenty będą wartościowane)
2(quote (1 2 3)) ; lista literalna (argumenty nie będą wartościowane)
3'(1 2 3) ; lista literalna (argumenty nie będą wartościowane)
(list 1 2 3) ; użycie funkcji list (argumenty będą wartościowane)
(quote (1 2 3)) ; lista literalna (argumenty nie będą wartościowane)
'(1 2 3) ; lista literalna (argumenty nie będą wartościowane)
Wewnętrznie obiekty typu PersistentList są listami dwukierunkowymi (ang. doubly
linked lists), chociaż cecha ta jest ukrywana przed programistą. Poza tym w Clojure
lista (jak większość struktur danych) jest niemutowalna, tzn. chcąc wprowadzić
zmianę w jej strukturze nigdy nie modyfikuje się reprezentującego ją obiektu, lecz
wytwarza nowy, który różni się od poprzedniego.
Zobacz także:
„Listy”, rozdział IX.
Sekwencje i obiekty Cons
Poza hermetycznymi listami w Clojure znajdziemy również obiekty typu Cons
(a dokładniej clojure.lang.Cons). Są one najbliższym odpowiednikiem komórek cons
znanych z innych dialektów języka Lisp. Dokładniej rzecz ujmując, z użyciem cons
możemy konstruować tzw. sekwencje (ang. sequences), czyli abstrakcyjne
kolekcje, które cechuje jednolity interfejs dostępu w postaci trzech podstawowych
operacji:
- odczyt wartości przechowywanej w komórce,
- odczyt następnej komórki połączonej z bieżącą,
- przyłączanie nowej komórki do istniejącej.
Odniesienia do wartości dowolnych typów możemy umieszczać w obiektach Cons i łączyć
w sekwencje z użyciem funkcji cons. Przyjmuje ona dwa argumenty: wartość
i obiekt, który również wyposażono w sekwencyjny interfejs (zaliczamy do nich
m.in. listy, wektory i mapy). Wartością zwracaną będzie komórka Cons, dla
której następną będzie podana jako argument.
Jeżeli podanym istniejącym obiektem będzie nil, zwrócona zostanie
jednoelementowa lista.
1(def pierwszy (cons 3 nil)) ; powstaje lista (3)
2(def drugi (cons 2 pierwszy)) ; powstaje cons(2)-->(3)
3(def ostatni (cons 1 drugi)) ; powstaje cons(1)-->cons(2)-->(3)
4
5(first ostatni) ; => 1 ; wartość w ostatnio dodanej
6(first (rest ostatni)) ; => 2 ; wartość w kolejnej
(def pierwszy (cons 3 nil)) ; powstaje lista (3)
(def drugi (cons 2 pierwszy)) ; powstaje cons(2)-->(3)
(def ostatni (cons 1 drugi)) ; powstaje cons(1)-->cons(2)-->(3)
(first ostatni) ; => 1 ; wartość w ostatnio dodanej
(first (rest ostatni)) ; => 2 ; wartość w kolejnej
Z użyciem Cons możemy zespolić nie tylko pojedyncze wartości, ale również
kolekcje (np. zwykłe listy). Mamy wtedy do czynienia ze
strukturą złożoną, którą można wyrazić na przykład tak:
(cons (list 1 2 3)
(cons (list 4 5 6)
(cons 10
())))
; => ((1 2 3) (4 5 6) 10)
Powyższe struktury bywają wykorzystywane do szybkiego łączenia już zgrupowanych wartości w większe zestawy, które dopiero podczas odczytywania są wypłaszczane, aby uzyskiwać indywidualne wartości.
(flatten
(cons '(1 2 3) (cons '(4 5 6) (cons 10 nil))))
; => (1 2 3 4 5 6 10)
Zobacz także:
„Komórki cons”, rozdział X.
Wektory
Wektor (ang. vector) to uporządkowana kolekcja wartości indeksowana z użyciem liczb całkowitych począwszy od 0 (pierwszy element). W kodzie programu do wyrażania wektorów używamy literału wektorowego, możemy też posłużyć się kilkoma wbudowanymi funkcjami.
Wektory są w Clojure reprezentowane obiektami typu
clojure.lang.PersistentVector. Cechuje je bardzo szybkie wyszukiwanie danych
i dodawanie nowych elementów do ich końców. Wektory są również funkcjami – przyjmują
jeden argument – numer indeksu, którego wartość elementu będzie zwrócona.
;; tworzenie wektora (funkcja)
(vector 1 2 3 4)
;=> [1 2 3 4]
;; tworzenie wektora z S-wyrażenia (literał)
[1 2 3 4]
;=> [1 2 3 4]
;; tworzenie wektora z innej kolekcji
(vec (list 1 2 3 4))
;=> [1 2 3 4]
;; przeszukiwanie wektora (element o indeksie 0)
([1 2 3 4] 0)
;=> 1
;; tworzenie wektora (funkcja)
(vector 1 2 3 4)
;=> [1 2 3 4]
;; tworzenie wektora z S-wyrażenia (literał)
[1 2 3 4]
;=> [1 2 3 4]
;; tworzenie wektora z innej kolekcji
(vec (list 1 2 3 4))
;=> [1 2 3 4]
;; przeszukiwanie wektora (element o indeksie 0)
([1 2 3 4] 0)
;=> 1
Zobacz także:
- „Wektory”, rozdział IX.
Mapy
Mapa (ang. map) to asocjacyjna kolekcja, która przechowuje odwzorowania kluczy na wartości. Klucze i wartości mogą być danymi dowolnego typu, jednak ten sam klucz musi być niepowtarzalny w obrębie danej mapy. Przeszukiwanie map w celu znalezienia wartości identyfikowanej kluczem jest bardzo szybkie, podobnie jak dodawanie nowych elementów.
W Clojure mapy reprezentowane są następującymi typami danych:
clojure.lang.PersistentHashMap(mapa bazująca na tablicach mieszających),clojure.lang.PersistentArrayMap(mapa bazująca na zwykłych tablicach),clojure.lang.PersistentTreeMap(mapa sortowana).
W kodzie programu do wyrażania map używamy literału mapowego w postaci
nawiasów klamrowych zawierających pary wyrażeń. Możemy też skorzystać z funkcji
hash-map, aby wyrazić pary kolejnymi argumentami wywołania.
;; tworzenie mapy (funkcja)
(hash-map :a 1 :b 2)
;=> {:a 1 :b 2}
;; tworzenie mapy sortowanej (funkcja)
(sorted-map :a 1 :b 2)
;=> {:a 1 :b 2}
;; tworzenie mapy z S-wyrażenia (literał)
{:a 1 :b 2}
;=> {:a 1 :b 2}
;; tworzenie mapy z S-wyrażenia (literał)
{:a 1 :b (+ 1 1)}
;=> {:a 1 :b 2}
;; tworzenie mapy z dwóch sekwencyjnych kolekcji
(zipmap [:a :b] [1 :b 2])
;=> {:a 1 :b 2}
;; tworzenie mapy z sekwencji par
(into {} [[:a 1] [:b 2]])
;=> {:a 1 :b 2}
;; tworzenie mapy z sekwencji
(apply hash-map [:a 1 :b 2])
;=> {:a 1 :b 2}
;; tworzenie mapy (funkcja)
(hash-map :a 1 :b 2)
;=> {:a 1 :b 2}
;; tworzenie mapy sortowanej (funkcja)
(sorted-map :a 1 :b 2)
;=> {:a 1 :b 2}
;; tworzenie mapy z S-wyrażenia (literał)
{:a 1 :b 2}
;=> {:a 1 :b 2}
;; tworzenie mapy z S-wyrażenia (literał)
{:a 1 :b (+ 1 1)}
;=> {:a 1 :b 2}
;; tworzenie mapy z dwóch sekwencyjnych kolekcji
(zipmap [:a :b] [1 :b 2])
;=> {:a 1 :b 2}
;; tworzenie mapy z sekwencji par
(into {} [[:a 1] [:b 2]])
;=> {:a 1 :b 2}
;; tworzenie mapy z sekwencji
(apply hash-map [:a 1 :b 2])
;=> {:a 1 :b 2}
Zobacz także:
- „Mapy”, rozdział IX.
Zbiory
Zbiór (ang. set) jest strukturą danych, która pozwala przechowywać elementy o dowolnych wartościach z zastrzeżeniem, że dana wartość może pojawić się w zbiorze tylko raz. Zbiory cechuje bardzo szybkie dodawanie i wyszukiwanie elementów. W Clojure istnieją wbudowane funkcje przeznaczone do przeprowadzania operacji na zbiorach, np. złączenie, projekcja, suma itd.
Zbiory reprezentowane są obiektami następujących typów danych:
clojure.lang.PersistentSet(zbiór bazujący na tablicach mieszających),clojure.lang.PersistentTreeSet(zbiór sortowany).
;; tworzenie zbioru (funkcja)
(hash-set :a :b :c)
;=> #{:a :b :c}
;; tworzenie zbioru sortowanego (funkcja)
(sorted-set :a :b :c)
;=> #{:a :b :c}
;; tworzenie zbioru z S-wyrażenia (literał)
#{:a :b :c}
;=> #{:a :b :c}
;; tworzenie zbioru z S-wyrażenia (literał)
#{:a :b (keyword "c")}
;=> #{:a :b :c}
;; tworzenie zbioru z sekwencji
(set [:a :b :c])
;=> #{:a :b :c}
;; tworzenie zbioru (funkcja)
(hash-set :a :b :c)
;=> #{:a :b :c}
;; tworzenie zbioru sortowanego (funkcja)
(sorted-set :a :b :c)
;=> #{:a :b :c}
;; tworzenie zbioru z S-wyrażenia (literał)
#{:a :b :c}
;=> #{:a :b :c}
;; tworzenie zbioru z S-wyrażenia (literał)
#{:a :b (keyword "c")}
;=> #{:a :b :c}
;; tworzenie zbioru z sekwencji
(set [:a :b :c])
;=> #{:a :b :c}
Zobacz także:
- „Zbiory”, rozdział IX.
Funkcje
Funkcja (ang. function) to konstrukcja zawierająca kod, który w trakcie wywołania dokonuje obliczania wartości dla podanego zestawu argumentów (ang. arguments). W językach czysto funkcyjnych jest to jedyny rezultat użycia funkcji, a w pozostałych (m.in. w Clojure) funkcje mogą wywoływać tzw. efekty uboczne (ang. side effects), tzn. poza zwróceniem wartości wpływać na otoczenie (np. modyfikować wartość zmiennej globalnej czy korzystać z podsystemu wejścia/wyjścia).
Poza tym rezultat działań funkcji w Clojure może zależeć od otoczenia. Przykładem będzie odwoływanie się w obliczeniach do globalnych obiektów referencyjnych wyrażających pewien zmienny stan bądź korzystanie z wartości pochodzących z leksykalnego otoczenia definicji funkcji. W tym drugim przypadku funkcję taką nazwiemy domknięciem (ang. closure).
Definicja funkcji w Clojure składa się z listowego S-wyrażenia zawierającego:
- wektorowe S-wyrażenie definiujące listę argumentów (ang. argument list),
- jedno lub więcej S-wyrażeń stanowiących ciało funkcji (ang. function body).
W języku Clojure możemy również korzystać z funkcji wieloczłonowych, które mogą obsługiwać więcej, niż jeden zestaw argumentów. W ich przypadku składnia definicji będzie nieco inna.
Wartością zwracaną (ang. return value) funkcji jest obliczona wartość ostatniego S-wyrażenia z jej ciała (lub z ciała danej wartościowości w przypadku funkcji wieloczłonowej).
W Clojure do tworzenia funkcji anonimowych (ang. anonymous functions) używamy
formy specjalnej fn, a do tworzenia funkcji nazwanych (ang. named
functions) makra defn. Funkcje anonimowe to obiekty funkcyjne, które nie
mają nadanych nazw. Funkcje nazwane mają w Clojure nazwy wyrażone zmiennymi
globalnymi.
1(defn krzycz ; definicja funkcji nazwanej
2 [napis] ; wektor z argumentami
3 (print napis "!")) ; wywołanie print z parametrem napis
4
5(krzycz "Witaj, Lispie") ; wywołanie funkcji z argumentem
6;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
7;=> nil ; zwracana wartość
(defn krzycz ; definicja funkcji nazwanej
[napis] ; wektor z argumentami
(print napis "!")) ; wywołanie print z parametrem napis
(krzycz "Witaj, Lispie") ; wywołanie funkcji z argumentem
;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
;=> nil ; zwracana wartość
Możemy też stworzyć wersję anonimową powyższej funkcji, jednak dla potrzeb przykładu musimy całą konstrukcję umieścić w S-wyrażeniu reprezentującym formę wywołania funkcji, aby móc zaobserwować rezultat jej działania:
1( ; forma wywołania funkcji
2 (fn ; definicja funkcji anonimowej
3 [napis] ; wektor z argumentami
4 (print napis "!")) ; wywołanie print z parametrem napis
5 "Witaj, Lispie!") ; argument wywołania funkcji
6
7;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
8;=> nil ; zwracana wartość
( ; forma wywołania funkcji
(fn ; definicja funkcji anonimowej
[napis] ; wektor z argumentami
(print napis "!")) ; wywołanie print z parametrem napis
"Witaj, Lispie!") ; argument wywołania funkcji
;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
;=> nil ; zwracana wartość
Powyższe można też wyrazić z użyciem literału funkcji anonimowej:
1( ; forma wywołania funkcji
2 #(print %1 "!") ; definicja i wywołanie print z pierwszym parametrem
3 "Witaj, Lispie!") ; argument wywołania funkcji
4
5;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
6;=> nil ; zwracana wartość
( ; forma wywołania funkcji
#(print %1 "!") ; definicja i wywołanie print z pierwszym parametrem
"Witaj, Lispie!") ; argument wywołania funkcji
;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
;=> nil ; zwracana wartość
Nic nie stoi też na przeszkodzie, aby zdefiniować funkcję anonimową, a następnie samodzielnie przypisać jej nazwę:
1(def krzycz ; definicja zmiennej globalnej
2 (fn ; definicja funkcji anonimowej
3 [napis] ; wektor z argumentami
4 (print napis "!"))) ; wywołanie print z parametrem napis
5
6(krzycz "Witaj, Lispie") ; wywołanie funkcji z argumentem
7;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
8;=> nil ; zwracana wartość
(def krzycz ; definicja zmiennej globalnej
(fn ; definicja funkcji anonimowej
[napis] ; wektor z argumentami
(print napis "!"))) ; wywołanie print z parametrem napis
(krzycz "Witaj, Lispie") ; wywołanie funkcji z argumentem
;=>> Witaj, Lispie! ; rezultat wywołania na ekranie
;=> nil ; zwracana wartość
W powyższym przykładzie definiujemy zmienną globalną krzycz, z wartością początkową
przypisaną do rezultatu wywołania formy specjalnej fn, którym będzie obiekt
funkcyjny (ang. function object) – reprezentacja istniejącej funkcji.
W Lispie funkcje są jednostkami pierwszej kategorii (ang. first-class citizens), tzn. wartościami, które mogą być traktowane tak, jak każde inne: przekazywane jako argumenty, albo zwracane jako rezultaty działania funkcji.
Zobacz także:
- „Funkcje i domknięcia”, rozdział VIII.
Wartości logiczne
Do wyrażania wartości logicznych w Clojure możemy użyć singletonów typu
java.lang.Boolean: true oznaczającego logiczną prawdę i false
oznaczającego logiczny fałsz. Wartości te zwracane są przez wbudowane predykaty
(funkcje, które na podstawie argumentów zwracają logiczną prawdę lub fałsz)
i konstrukcje warunkowe.
Wartość nieustalona
Literał wartości nieustalonej nil, której nazwa pochodzi od angielskiego określenia
not in list (pol. nie na liście), ma w Clojure specjalne znaczenie i służy
do wyrażania obiektu reprezentującego wartość nieustaloną lub brak
wartości. Wewnętrznie nil jest reprezentowany przez obecną w Javie wartość null
(wskaźnik pusty).
Konstrukt nil jest używany w Clojure do komunikowania, że dana forma nie zwraca
żadnej wartości, lub że wartości nie udało się uzyskać. Korzysta z niego wiele
wbudowanych funkcji i konstrukcji warunkowych. W przypadku tych pierwszych nil
oznacza brak wyniku (wartość zwracana) bądź domyślną wartość początkową (przyjmowany
argument), a w przypadku drugich odpowiada logicznej wartości fałszu
(false). Ponadto w obsłudze sekwencji wartość nil jest
wykorzystywana do oznaczenia ich końców.
Komentarze
Komentarze w programach komputerowych służą do objaśniania fragmentów kodu źródłowego w języku naturalnym. Mogą pełnić funkcję dokumentacyjną lub zawierać notatki dotyczące postępów w realizacji pewnych zadań. Czasami też wykorzystuje się je do zaprezentowania rezultatów obliczeń przykładowych form.
W Clojure komentarz rozpoczynamy znakiem średnika ;, po którym umieszczamy dowolny
tekst. Komentarzem będzie dowolna sekwencja znaków, aż do końca linii, w której go
rozpoczęto:
1(print "Witaj, Lispie!") ; to jest komentarz
2
3;; To jest dłuższy komentarz
4;; zapisany zgodnie z konwencją
5;; poprzedzania każdej linii
6;; dwoma średnikami.
7
8;; Poniższe komentarze
9;; służą prezentowaniu rezultatów obliczeń.
10;;
11(+ 2 2) ; => 4
12(- 2 2) ; => 0
13
14(+ 2 2)
15; => 4
16
17'(1 2 3)
18; => (1 2 3)
(print "Witaj, Lispie!") ; to jest komentarz
;; To jest dłuższy komentarz
;; zapisany zgodnie z konwencją
;; poprzedzania każdej linii
;; dwoma średnikami.
;; Poniższe komentarze
;; służą prezentowaniu rezultatów obliczeń.
;;
(+ 2 2) ; => 4
(- 2 2) ; => 0
(+ 2 2)
; => 4
'(1 2 3)
; => (1 2 3)
Forma komentująca
Poza komentarzami składniowymi, wyrażanymi średnikiem, w Clojure istnieje specjalne makro, które pozwala wyłączać obliczanie wskazanego S-wyrażenia:
(comment
(print "Witaj, Lispie!")
123)
(comment
(print "Witaj, Lispie!")
123)
Warto zauważyć, że comment jest konstrukcją, której jako argumenty należy przekazać
poprawne składniowo symboliczne wyrażenia.
Wartością zwracaną przez makro jest nil.
Ignorowanie następnej formy
Kolejnym sposobem na wyłączanie części programu z procesu obliczania wartości jest
użycie makra czytnika #_. Powoduje ono, że następna umieszczona po nim forma nie
będzie wartościowana:
#_ (print "Witaj, Lispie!") ; wyłącza formę wywołania funkcji
(#_#_ print "Witaj, Lispie!") ; wyłącza dwie pierwsze zagnieżdżone formy
(print #_ "Witaj, Lispie!") ; wyłącza formę stałą "Witaj, Lispie!"
[#_#_ 1 2 3] ; wyłącza dwie zagnieżdżone formy stałe 1 i 2
#_ (print "Witaj, Lispie!") ; wyłącza formę wywołania funkcji
(#_#_ print "Witaj, Lispie!") ; wyłącza dwie pierwsze zagnieżdżone formy
(print #_ "Witaj, Lispie!") ; wyłącza formę stałą "Witaj, Lispie!"
[#_#_ 1 2 3] ; wyłącza dwie zagnieżdżone formy stałe 1 i 2
Konstrukcje sterujące
Clojure wyposażono w wiele form specjalnych i makr, które służą do sterowania procesem wartościowania wyrażeń, m.in. kolejnością, liczbą powtórzeń czy warunkowaniem przetwarzania.
Wyrażenia warunkowe
Znane z języków imperatywnych instrukcje warunkowe w Lispach mają odpowiedniki jako warunkowe formy specjalne lub makra. Forma specjalna i makro tym różnią się od funkcji, że przekazywane do nich wybrane argumenty mogą być wartościowane lub nie (zależnie od konkretnej formy) przed wywołaniem podprogramu. Dzięki tej cesze możliwe jest budowanie m.in. takich wyrażeń, w których obliczenie wartości pewnych argumentów zależy od rezultatu obliczenia innych (wcześniejszych). Można więc sterować tym, czy i kiedy zadziała zasada przekazywania przez wartość, a tym samym budować konstrukcje warunkowe bądź pętle.
Formy specjalne i makra będą omówione później, a podstawowa różnica między nimi jest taka, że makra są elementem języka pozwalającym dokonywać przekształceń kodu źródłowego, natomiast formy specjalne wbudowanymi w ewaluator konstrukcjami. Zarówno jedne, jak i drugie mogą mieć odmienne od przyjętego sposoby wartościowania i przekazywania argumentów czy wpływania na otoczenie (stany innych pamięciowych obiektów).
Wykonywanie warunkowe, if
Forma specjalna if służy do warunkowego obliczania wyrażeń.
Użycie:
(if predykat wyrażenie-prawda wyrażenie-fałsz?).
Forma if przyjmuje dwa obowiązkowe argumenty. Pierwszym jest warunek do
przeliczenia, który (jeżeli nie będzie przyjmował ani wartości false ani
nil) sprawi, że kolejny argument zostanie również obliczony. Jeżeli podano
opcjonalny trzeci argument, będzie on obliczony tylko wtedy, gdy pierwszy argument
ma wartość false lub nil.
Forma specjalna if zwraca wartość ostatnio obliczonego wyrażenia lub nil,
jeżeli nie podano trzeciego argumentu, a pierwsze wyrażenie zwróciło logiczny
fałsz.
if
(if (= 2 2)
"równe"
"różne")
; => "równe"
Wraz z formą if często wykorzystywane jest makro and, które służy do
wyrażania operacji koniunkcji logicznej (iloczynu logicznego). Dokonuje ono
obliczania wartości wyrażeń podanych jako jego argumenty (w porządku występowania),
dopóki ich wartością jest logiczna prawda (nie wartość false i nie
nil). Zwracaną wartością jest wtedy wartość ostatnio podanego
wyrażenia. Jeżeli któreś z wyrażeń zwróci wartość false lub nil, przetwarzanie
kolejnych argumentów zostaje wstrzymane i zwracana jest jego wartość.
and
(if (and (= 2 2) (< 2 3)) true)
; => true
Innym makrem, które znajdziemy w towarzystwie if jest or. Służy ono do
wyrażania operacji sumy logicznej (logicznej alternatywy). Makro to oblicza
wartości kolejnych wyrażeń podanych jako jego argumenty (w kolejności występowania)
do momentu, aż wartością któregoś będzie logiczna prawda (nie wartość
false i nie nil). Zwracaną wartością jest wtedy wartość ostatnio
przetwarzanego wyrażenia. Jeżeli wartości wszystkich wyrażeń to false lub
nil, zwracana jest wartość ostatniego podanego wyrażenia (false lub
nil).
or
(if (or (= 2 2) (< 4 3)) true)
; => true
Wykonywanie warunkowe, if-not
Makro if-not jest odwrotną wersją formy specjalnej if.
Użycie:
(if-not predykat wyrażenie-fałsz wyrażenie-prawda?).
Makro przyjmuje dwa obowiązkowe argumenty. Pierwszym jest warunek do
przeliczenia, który jeżeli będzie przyjmował wartość logicznego fałszu (false
lub nil), sprawi, że kolejny argument zostanie również obliczony. Jeżeli podano
opcjonalny trzeci argument, będzie on obliczony tylko wtedy, gdy pierwszy
argument reprezentuje logiczną prawdę (ma wartość różną od false
i różną od nil).
Makro if-not zwraca wartość ostatnio obliczonego wyrażenia lub nil, jeżeli
nie podano trzeciego argumentu, a pierwsze wyrażenie zwróciło logiczną prawdę.
if-not
(if-not (= 2 2)
"różne"
"równe")
; => "równe"
Wykonywanie warunkowe, when
Makro when działa podobnie do konstrukcji if, przy czym jest nieco
prostsze, ponieważ nie ma w nim miejsca na wyrażenie alternatywne (wykonywane, gdy
podany warunek nie jest spełniony).
Użycie:
(when predykat & wyrażenie…).
Pierwszy argument powinien być formą wyrażającą warunek logiczny (zwracającą
true lub false, ew. nil), a każdy pozostały będzie
potraktowany jak wyrażenie, które zostanie obliczone, gdy wartością zwracaną przez
konstrukcję warunkową będzie logiczna prawda (wartość różna od false i różna od
nil).
when
1(when (= 2 2)
2 (println "można podać")
3 (println "wiele wyrażeń"))
4
5; >> można podać
6; >> wiele wyrażeń
(when (= 2 2)
(println "można podać")
(println "wiele wyrażeń"))
; >> można podać
; >> wiele wyrażeń
Wykonywanie warunkowe, when-not
Makro when-not jest odwrotną wersją makra when.
Użycie:
(when-not predykat & wyrażenie…).
Pierwszy argument powinien być predykatem, a każdy pozostały będzie potraktowany
jak wyrażenie, które zostanie obliczone, gdy wartością predykatu będzie logiczny
fałsz (wartość false lub nil).
when-not
1(when-not (= 2 1)
2 (println "można podać")
3 (println "wiele wyrażeń"))
4
5; >> można podać
6; >> wiele wyrażeń
(when-not (= 2 1)
(println "można podać")
(println "wiele wyrażeń"))
; >> można podać
; >> wiele wyrażeń
Lista warunków, cond
Makro cond pozwala zapisać listę warunków z przypisanymi do niej wyrażeniami, które
zostaną obliczone, gdy dany warunek będzie spełniony.
Użycie:
(cond & para…),
gdzie para to:
predykat wyrażenie,:else wyrażenie-domyślne.
Makro przyjmuje parzystą liczbę argumentów. Dla każdej pary sprawdza, czy podane
wyrażenie warunkowe zwraca wartość różną od false i od nil. Jeżeli tak jest,
wartościowany będzie przypisany mu argument z pary (wyrażenie) i przetwarzanie
dalszych argumentów zostanie wstrzymane, a zwracaną wartością będzie wartość
obliczonego wyrażenia.
Opcjonalnie można dodać ostatnią parę (opcję), której pierwszy element równy będzie
:else. Przypisane mu wyrażenie zostanie obliczone, gdy żadne wcześniejsze nie
zakończyło pracy. Pozwala to ustawiać domyślną wartość zwracaną.
Jeżeli nie podano opcji domyślnej, a żaden warunek nie był spełniony, zwracaną
wartością będzie nil.
cond
1(cond
2 (= 2 3) "2 i 3 są równe"
3 (< 2 3) "2 jest mniejsze niż 3"
4 :else "nic")
5
6; => "2 jest mniejsze niż 3"
(cond
(= 2 3) "2 i 3 są równe"
(< 2 3) "2 jest mniejsze niż 3"
:else "nic")
; => "2 jest mniejsze niż 3"
Lista przypadków, case
Forma specjalna case działa podobnie do cond, ale zamiast wyrażeń
warunkowych w opcjach należy podawać stałe wartości, które będą dopasowywane do
wartości pierwszego przekazanego argumentu wywołania.
Użycie:
(case wartość opcja…),
gdzie opcja to:
wartość wyrażenie,(wartość…) wyrażenie,wyrażenie-domyślne.
Jeżeli chcemy porównywać podaną wartość z wieloma z serii dla każdej z możliwych opcji, należy tę serię możliwości zapisać w postaci listowego S-wyrażenia.
Wartości, z którymi porównywana będzie wartość pierwszego argumentu muszą być formami stałymi, ponieważ są opracowywane w trakcie kompilacji. Możemy więc podawać literały czy inne atomowe reprezentacje, które wyrażają własne wartości. Wyrażenia do obliczenia w przypadku pozytywnego przejścia testu mogą z kolei przedstawiać dowolne formy.
Opcjonalnie możliwe jest podanie jako ostatniego argumentu wyrażenia, które zostanie obliczone, jeżeli badana wartość nie spełni żadnego z wcześniej podanych warunków. Warto z tej możliwości korzystać, ponieważ w przeciwnym wypadku program zgłosi wyjątek, gdy żadne z dopasowań nie będzie spełnione.
case
1(def x 'herbatniki) ; x odnosi się do symbolu herbatniki
2
3(case x
4 "" "nic"
5 (draże miętusy) "cukierki"
6 (herbatniki pierniki) "ciastka"
7 (str x " to produkt nieznany"))
8
9; => "ciastka"
(def x 'herbatniki) ; x odnosi się do symbolu herbatniki
(case x
"" "nic"
(draże miętusy) "cukierki"
(herbatniki pierniki) "ciastka"
(str x " to produkt nieznany"))
; => "ciastka"
Warto zauważyć, że symbole i listy nie zostały zacytowane. To właśnie właściwość form specjalnych – pewne wyrażenia nie są wartościowane, nie zachodzi więc konieczność stosowania specjalnych zabiegów, które zapobiegałyby wartościowaniu.
Lista warunków z predykatem, condp
Makro condp działa podobnie jak cond, ale jest o wiele bardziej
elastyczne.
Użycie:
(condp predykat wyrażenie & para…)
Jako pierwszy argument należy podać predykat, czyli funkcję, która powinna zwracać wartość logiczną, a jako drugi wyrażenie. Kolejne, nieobowiązkowe argumenty to składające się z par opcje, które mogą być wyrażone następującymi zapisami:
wyrażenie-testowe wyrażenie-wynikowe,wyrażenie-testowe :>> funkcja-wynikowa,wyrażenie-domyślne.
Symboliczny zapis :>> to słowo kluczowe, które ma w kontekście makra
condp specjalne znaczenie.
Dla każdej podanej opcji będzie wartościowana przypisana jej forma wywołania funkcji:
(predykat wyrażenie-warunkowe wyrażenie).
Predykat będzie wywoływany dla każdej podanej w kolejności opcji z dwoma przekazywanymi argumentami. Pierwszy będzie wartością wyrażenia testowego danej opcji, a drugi wyrażeniem podanym jako argument wywołania całego makra.
Jeżeli predykat zwróci wartość odpowiadającą logicznej prawdzie (różną od false
i różną od nil), sprawdzanie kolejnych opcji zakończy się i zostanie zwrócone
wyrażenie wynikowe przypisane do bieżącej opcji lub wartość powstała na skutek
wywołania funkcji wynikowej (w przypadku, gdy użyto słowa kluczowego
:>>). W tym ostatnim przypadku do funkcji (która powinna przyjmować jeden argument)
zostanie przekazana wartość zwracana przez predykat.
W przypadku, gdy jako ostatnią z opcji podano dodatkowe wyrażenie
(wyrażenie-domyślne), jego wartość zostanie zwrócona, jeżeli żadna z opcji nie
zostanie dopasowana do podanych danych. Gdy taka sytuacja wystąpi, ale nie podano
domyślnego wyrażenia, zwróconą wartością będzie nil.
condp
1(condp
2 = ; predykat
3 (+ 2 2) ; wyrażenie (da w wyniku 4)
4 1 "jeden" ; opcja 1: łańcuch znakowy
5 2 "dwa" ; opcja 2: łańcuch znakowy
6 3 "trzy" ; opcja 3: łańcuch znakowy
7 4 "cztery" ; opcja 4: łańcuch znakowy
8 "żadna") ; wyrażenie opcji domyślnej
9
10; => "cztery"
(condp
= ; predykat
(+ 2 2) ; wyrażenie (da w wyniku 4)
1 "jeden" ; opcja 1: łańcuch znakowy
2 "dwa" ; opcja 2: łańcuch znakowy
3 "trzy" ; opcja 3: łańcuch znakowy
4 "cztery" ; opcja 4: łańcuch znakowy
"żadna") ; wyrażenie opcji domyślnej
; => "cztery"
Dostęp do składowych Javy
Dostęp do składowej, .
Forma specjalna . to w Clojure sposób na dostęp do obiektów Javy. Jest to de
facto operator wyboru składowej (ang. member-access operator).
-
Gdy pierwszym argumentem jest symbol nazywający klasę Javy, ewaluator potraktuje zapis tak, jakby chodziło o dostęp do statycznej składowej tej klasy.
-
Jeżeli pierwszym argumentem nie jest nazwa klasy Javy, ewaluator uzna, że jest to instancja klasy, na której chcemy wywołać metodę lub uzyskać dostęp do wartości jej pola. Gdy nie podano większej liczby argumentów, będzie to pole, chyba że istnieje publiczna metoda o podanej nazwie nieprzyjmująca argumentów – w takim przypadku to ona zostanie wywołana. Jeżeli istnieje zarówno pole o podanej nazwie, jak i metoda, wtedy poprzedzenie symbolicznej nazwy znakiem łącznika (
-) będzie oznaczało, że chodzi o pole. -
Jeżeli podano kolejne argumenty poza pierwszym, wywołana zostanie metoda instancji o podanej jako pierwszy argument nazwie. Dodatkowe argumenty zostaną (od lewej do prawej) przekazane do wywołania po ewaluacji ich wartości.
Dodatkowe argumenty mogą być też listowym S-wyrażeniem. W takim przypadku na pierwszym miejscu powinien znajdować się symbol identyfikujący metodę do wywołania.
Istnieje też uproszczona wersja tej formy specjalnej, gdzie kropka wchodzi w skład symbolicznej nazwy składowej obiektu, który jest podany jako kolejny argument.
.
(. " a " trim) ; => a
(.trim " a ") ; => a
(. "abc" substring 0 1) ; => a
(. "abc" (substring 0 1)) ; => a
(. " a " trim) ; => a
(.trim " a ") ; => a
(. "abc" substring 0 1) ; => a
(. "abc" (substring 0 1)) ; => a
Dostęp do składowych, ..
Makro o nazwie .. jest lukrem składniowym i pozwala wyrażać zagnieżdżony dostęp
do składowych obiektów Javy w czytelny sposób. Efektem jego użycia jest stworzenie
kaskady wywołań omówionej wyżej formy specjalnej ..
W praktyce .. wykonuje serię wywołań metod, w której wynik jednej staje się
obiektem wejściowym dla kolejnej. Każde wyrażenie po .. jest interpretowane
podobnie jak w formie ., ale bez konieczności ręcznego zagnieżdżania.
..
(.. " a " trim length) ; => 1
(.. " a " trim length toString (replace "1" "X")) ; => "X"
(.. " a " trim length) ; => 1
(.. " a " trim length toString (replace "1" "X")) ; => "X"
Organizowanie kodu
W funkcyjnym programie każda konstrukcja jest wyrażeniem, które daje się obliczyć i zwraca jakąś wartość, nie generując efektów ubocznych. Jednak są klasy problemów, które rozwiązywane w sposób czysto funkcyjny powodowałyby powstawanie nieczytelnego lub mało wydajnego kodu. Dialekty języka Lisp są więc tolerancyjne pod względem sposobu reprezentowania algorytmów i pozwalają wyrażać rozwiązania problemów na różne sposoby, oferując między innymi konstrukcje sterujące znane z imperatywnych języków programowania.
Grupowanie S-wyrażeń, do
Chyba najbardziej powszechną konstrukcją, która pozwala na chwilę zapomnieć o tym, że
mamy do czynienia z wartościowanymi wyrażeniami i potraktować elementy programu jak
instrukcje jest forma specjalna do. Służy ona do grupowania wielu wyrażeń w taki
sposób, że tylko wartość ostatniego zostanie zwrócona, chociaż ewentualne efekty
uboczne (np. wyświetlanie tekstu na ekranie) będą mogły powstawać we wszystkich.
Użycie:
(do & wyrażenie…).
Forma specjalna do przyjmuje zero lub więcej S-wyrażeń, które będą obliczone
w kolejności ich podawania. Wartością zwracaną będzie rezultat obliczenia
wartości stałej ostatniego z nich.
Jeżeli nie podamy żadnego S-wyrażenia, wartością zwracaną będzie nil.
do
1(do)
2; => nil
3
4(do 123 456)
5; => 456
6
7(do
8 (println "test")
9 123
10 (+ 1 1)
11 (+ 2 2))
12; >> test
13; => 4
(do)
; => nil
(do 123 456)
; => 456
(do
(println "test")
123
(+ 1 1)
(+ 2 2))
; >> test
; => 4
Przyłączanie argumentu, doto
Makro doto pozwala przyłączać podaną wartość jako pierwszy argument wywołania
podanych wyrażeń. Najczęściej bywa używane, aby w przejrzysty sposób reprezentować
wywołania metod Javy lub wtedy, gdy chcemy, żeby wartością zwracaną była wartość
pierwszego argumentu wywołania jakiejś funkcji, makra lub formy specjalnej.
(doto wartość & wyrażenie…).
Makro przyjmuje jeden obowiązkowy argument, którym powinna być dowolna wartość. Każdy kolejny argument będzie potraktowany jak S-wyrażenie, które przed wartościowaniem zostanie przekształcone w taki sposób, że w miejsce jego pierwszego argumentu wywołania będzie podstawiona właśnie ta wartość.
Wartością zwracaną przez makro doto jest wartość przekazana jako pierwszy argument.
doto
1(doto 2
2 (println "za pierwszym razem")
3 (println "za drugim razem"))
4
5; >> 2 za pierwszym razem
6; >> 2 za drugim razem
7; => 2
8
9(doto (java.util.ArrayList.)
10 (.add 1)
11 (.add 2)
12 (.add 3))
13
14; => [1 2 3]
(doto 2
(println "za pierwszym razem")
(println "za drugim razem"))
; >> 2 za pierwszym razem
; >> 2 za drugim razem
; => 2
(doto (java.util.ArrayList.)
(.add 1)
(.add 2)
(.add 3))
; => [1 2 3]
Liczenie czasu, time
Makro time pozwala nam wyświetlić czas wykonania podanego wyrażenia. Przydaje
się, gdy chcemy optymalizować fragmenty programu pod kątem wydajnościowym.
Użycie:
(time wyrażenie).
Argumentem makra powinno być S-wyrażenie, którego wartość będzie obliczona. Można
użyć do, jeżeli chcemy podać więcej wyrażeń.
Wartością zwracaną makra time jest wartość przeliczonego wyrażenia, które podano.
Efektem ubocznym wywołania makra jest wyświetlenie na standardowym wyjściu raportu z czasu wykonywania podanego wyrażenia.
time
1(time 123)
2; >> "Elapsed time: 0.012667 msecs"
3; => 123
4
5(time (Thread/sleep 500))
6; >> "Elapsed time: 505.079375 msecs"
7; => nil
(time 123)
; >> "Elapsed time: 0.012667 msecs"
; => 123
(time (Thread/sleep 500))
; >> "Elapsed time: 505.079375 msecs"
; => nil
Przewlekanie, ->
Makro przewlekania (ang. threading macro), zwane też makrem przewlekania pierwszych argumentów (ang. thread-first macro), umożliwia przedstawianie kodu źródłowego z zagnieżdżonymi wywołaniami w bardziej czytelny sposób. Jego działanie polega na przyjęciu zestawu S-wyrażeń i potraktowaniu każdego poza pierwszym jako formy wywołania (nawet, jeżeli nie ujęto go w nawiasy), a następnie wstawianiu w miejsce pierwszego argumentu każdej z form wartości zwracanej przez wywołanie umieszczone wcześniej. Dzięki temu możemy na chwilę zapomnieć o notacji polskiej.
Użycie:
(-> wyrażenie & wyrażenie…).
Argumentami makra są S-wyrażenia (przynajmniej jedno), a wartością zwracaną jest wartość ostatniego przekazanego S-wyrażenia.
->
1(-> [1 2 3 4] ; rezultat [1 2 3 4]
2 last ; rezultat (last [1 2 3 4]) => 4
3 (- 2) ; rezultat (- 4 2) => 2
4 println ; rezultat (println 2) => nil
5)
6
7; >> 2
(-> [1 2 3 4] ; rezultat [1 2 3 4]
last ; rezultat (last [1 2 3 4]) => 4
(- 2) ; rezultat (- 4 2) => 2
println ; rezultat (println 2) => nil
)
; >> 2
Spójrzmy na te same operacje uszeregowane w kodzie bez używania makra:
(println
(- (last
[1 2 3 4]))
2)
; => nil
; >> 2
Porównajmy obydwa zapisy w postaciach bardziej kompaktowych:
1(println (- (last [1 2 3 4])) 2) ; od środka do zewnątrz
2(-> [1 2 3 4] last (- 2) println) ; z lewa do prawa
(println (- (last [1 2 3 4])) 2) ; od środka do zewnątrz
(-> [1 2 3 4] last (- 2) println) ; z lewa do prawa
Łatwo zauważyć różnicę: w pierwszym będziemy obliczali wartości od najbardziej zagnieżdżonych do obejmujących, a w drugim od lewej do prawej (z rezultatem podstawianym za każdym razem jako pierwszy argument).
Przewlekanie ostatnich, ->>
Makro przewlekania ostatnich argumentów (ang. thread-last macro) działa podobnie do makra przewlekania, lecz wartość każdego poprzedniego S-wyrażenia nie będzie podstawiana jako pierwszy, ale jako ostatni argument kolejnego.
Użycie:
(->> wyrażenie & wyrażenie…).
Argumentami makra są S-wyrażenia (przynajmniej jedno), a wartością zwracaną jest wartość ostatniego przekazanego S-wyrażenia.
->>
1(->> [1 2 3 4] ; rezultat [1 2 3 4]
2 last ; rezultat (last [1 2 3 4]) => 4
3 (- 2) ; rezultat (- 2 4) => -2
4 println ; rezultat (println -2) => nil
5)
6
7; => nil
8; >> -2
(->> [1 2 3 4] ; rezultat [1 2 3 4]
last ; rezultat (last [1 2 3 4]) => 4
(- 2) ; rezultat (- 2 4) => -2
println ; rezultat (println -2) => nil
)
; => nil
; >> -2
W powyższym przykładzie widzimy, że różnica w obliczeniach w stosunku do przykładów poprzednich pojawia się w linii nr 3. Dochodzi do zamiany argumentów odejmowania z powodu podstawienia wartości jako drugi argument odejmowania.
Przewlekanie wartościowych, some->
Makro some-> działa podobnie do makra ->, lecz mamy do czynienia
z natychmiastowym zatrzymaniem przewlekania i dalszego wartościowania wyrażeń, gdy
którekolwiek z łańcucha zwróci nil. W związku z tym makro przewlekania rezultatów
wartościowych stosowane bywa tam, gdzie któraś forma może zwrócić wartość
nieustaloną, np. w rezultatach przeszukiwania kolekcji czy dostępie do metod Javy,
które, gdyby wywołać z argumentem nil spowodują powstanie wyjątku.
Użycie:
(some-> wyrażenie & wyrażenie…).
Argumentami makra są S-wyrażenia (przynajmniej jedno), a wartością zwracaną jest
wartość ostatniego przekazanego S-wyrażenia lub nil, jeżeli wartością któregoś
będzie nil.
some->
1(some-> [1 2 3 4] ; rezultat [1 2 3 4]
2 get 50 ; rezultat (get [1 2 3 4] 50) => nil
3 (+ 2) ; brak wartościowania
4 println ; brak wartościowania
5)
6
7; => nil
(some-> [1 2 3 4] ; rezultat [1 2 3 4]
get 50 ; rezultat (get [1 2 3 4] 50) => nil
(+ 2) ; brak wartościowania
println ; brak wartościowania
)
; => nil
Widzimy, że w linii nr 2 doszło do przerwania dalszego wartościowania S-wyrażeń
z łańcucha, ponieważ forma (get [1 2 3 4] 50) zwróciła nil (przy próbie dostępu
do nieistniejącego elementu o indeksie 50). Spójrzmy co by się stało, gdyby zamiast
some-> użyć ->:
1(-> [1 2 3 4] ; rezultat [1 2 3 4]
2 get 50 ; rezultat (get [1 2 3 4] 50) => nil
3 (+ 2) ; rezultat (+ nil 2) (wyjątek)
4 println ; brak wartościowania (wyjątek)
5)
6
7; >> java.lang.NullPointerException:
(-> [1 2 3 4] ; rezultat [1 2 3 4]
get 50 ; rezultat (get [1 2 3 4] 50) => nil
(+ 2) ; rezultat (+ nil 2) (wyjątek)
println ; brak wartościowania (wyjątek)
)
; >> java.lang.NullPointerException:
Zamiast uzyskać wartość nieustaloną nil program awaryjnie zakończył pracę
komunikując powstanie wyjątku Javy. Było to spowodowane próbą zsumowania nil
i liczby 2.
Przewlekanie wartościowych, some->>
Makro some->> działa podobnie do makra some->, ale wartości poprzednio
wyliczonych S-wyrażeń podstawiane są jako ostatnie argumenty kolejnych.
Użycie:
(some->> wyrażenie & wyrażenie…).
Argumentami makra są S-wyrażenia (przynajmniej jedno), a wartością zwracaną jest
wartość ostatniego przekazanego S-wyrażenia lub nil, jeżeli wartością któregoś
będzie nil.
some->>
1(some->> [2 4 6 8] ; rezultat [2 4 6 8]
2 (filter odd?) ; rezultat (filter odd? [2 4 6 8]) => ()
3 first ; rezultat (first ()) => nil
4 (+ 2) ; brak wartościowania
5 println ; brak wartościowania
6)
7
8; => nil
(some->> [2 4 6 8] ; rezultat [2 4 6 8]
(filter odd?) ; rezultat (filter odd? [2 4 6 8]) => ()
first ; rezultat (first ()) => nil
(+ 2) ; brak wartościowania
println ; brak wartościowania
)
; => nil
W linii nr 2 użyliśmy nieomawianej jeszcze funkcji filter. Dokonuje ona filtrowania
kolekcji podanej jako drugi argument, a do decydowania o tym, czy element zostanie
wpisany do wyjściowej struktury danych, czy pominięty, używa predykatu przekazanego
jako pierwszy argument wywołania.
Tu rolę predykatu pełni funkcja odd?, która zwraca logiczną prawdę, gdy wartość
przekazanego jej argumentu jest liczbą nieparzystą. W efekcie filter wygeneruje
pustą kolekcję, ponieważ wejściowa zawiera same liczby parzyste.
Wywołanie first w odniesieniu do pustej kolekcji zwróci nil i na tym przewlekanie
się zakończy. Gdybyśmy nie zastosowali makra some->>, wtedy S-wyrażenie (+ 2 nil)
doprowadziłoby do zgłoszenia wyjątku podczas wartościowania.
Przewlekanie warunkowe, cond->
Makro cond-> działa podobnie do ->, jednak S-wyrażenia interpretowane są
parami. Pierwsze z każdej pary jest wyrażeniem warunkowym, a drugie będzie
wartościowane wtedy, gdy pierwsze jest prawdziwe (jego wartością nie jest false ani
nil). Każde drugie wyrażenie par traktowane jest jak forma wywołania, nawet jeżeli
nie ujęto go w nawiasy.
Warunkowe przewlekanie pierwszego argumentu przydaje się do czytelnego wyrażenia zestawu obliczeń, które zależą od aktualnych warunków.
Użycie:
(cond-> wyrażenie & para…),
gdzie para to:
predykat wyrażenie.
Makro cond-> przyjmuje wyrażenie początkowe oraz pary S-wyrażeń, gdzie pierwsze
jest predykatem, a drugie będzie wartościowane w taki sposób, że jako pierwszy
argument będzie wstawiony rezultat wartościowania poprzedniego wyrażenia
z łańcucha. Wartością zwracaną jest wartość ostatnio obliczonego S-wyrażenia.
cond->
1(def dodaj-jeden? true)
2(def odejmij-jeden? false)
3
4(cond-> 123 ; rezultat 123
5 dodaj-jeden? inc ; rezultat (inc 123) => 124
6 odejmij-jeden? dec ; brak wartościowania
7 true println ; rezultat (println 124) => nil
8)
9
10; => nil
11; >> 124
(def dodaj-jeden? true)
(def odejmij-jeden? false)
(cond-> 123 ; rezultat 123
dodaj-jeden? inc ; rezultat (inc 123) => 124
odejmij-jeden? dec ; brak wartościowania
true println ; rezultat (println 124) => nil
)
; => nil
; >> 124
Przewlekanie warunkowe, cond->>
Makro warunkowego przewlekania ostatniego argumentu działa podobnie do cond->, ale
– jak wskazuje nazwa – dochodzi do podstawiania wartości ostatnio przeliczanego
S-wyrażenia w miejsce ostatniego argumentu wyrażenia aktualnie przeliczanego.
Warunkowe przewlekanie ostatniego argumentu przydaje się do czytelnego wyrażenia transformacji dokonywanych na kolekcjach, ponieważ wiele wbudowanych funkcji operujących na tego typu strukturach danych przyjmuje je jako ostatnie argumenty.
Użycie:
(cond->> wyrażenie & para…),
gdzie para to:
predykat wyrażenie.
Makro cond->> przyjmuje wyrażenie początkowe oraz pary S-wyrażeń, gdzie pierwsze
jest predykatem, a drugie będzie wartościowane w taki sposób, że jako pierwszy
argument będzie wstawiony rezultat wartościowania poprzedniego wyrażenia
z łańcucha. Wartością zwracaną jest wartość ostatnio obliczonego S-wyrażenia.
cond->
1(def parzyste? true)
2(def nieparzyste? false)
3
4(cond->> [1 2 3 4] ; [1 2 3 4]
5 parzyste? (filter even?) ; (filter even? [1 2 3 4]) => (2 4)
6 nieparzyste? (filter odd?) ; brak wartościowania
7 true println ; (println '(2 4)) => nil
8)
9
10; => nil
11; >> (2 4)
(def parzyste? true)
(def nieparzyste? false)
(cond->> [1 2 3 4] ; [1 2 3 4]
parzyste? (filter even?) ; (filter even? [1 2 3 4]) => (2 4)
nieparzyste? (filter odd?) ; brak wartościowania
true println ; (println '(2 4)) => nil
)
; => nil
; >> (2 4)
Wiązanie z nazwą, as->
Makro as-> służy do przewlekania rezultatów wyrażeń, ale zamiast ustalonej pozycji
mamy do czynienia z wytwarzaniem powiązań z symboliczną nazwą. Przydaje się to
w sytuacjach, gdy różne wywołania wymagają umieszczenia istotnego argumentu w różnych
miejscach.
Użycie:
(as-> wyrażenie symboliczna-nazwa & wyrażenie…).
Argumentami makra jest wyrażenie początkowe, którego wartość będzie powiązana z symboliczną nazwą (podaną jako drugi argument), a następnie przewlekana przez podane dalej S-wyrażenia w taki sposób, że wartość każdego z nich będzie powiązana z symboliczną nazwą przed wywołaniem kolejnego.
as->
1(as-> [1 2 3 4] wynik ; po podstawieniu wyniku:
2 (filter even? wynik) ; (filter even? [1 2 3 4])
3 (last wynik) ; (last [2 4])
4 [wynik (inc wynik)]) ; [4 5]
5
6; => [4 5]
(as-> [1 2 3 4] wynik ; po podstawieniu wyniku:
(filter even? wynik) ; (filter even? [1 2 3 4])
(last wynik) ; (last [2 4])
[wynik (inc wynik)]) ; [4 5]
; => [4 5]
Podsumowanie
Tłumaczenie kodu źródłowego
Poniższy diagram przedstawia poszczególne etapy tłumaczenia kodu źródłowego programu z postaci tekstowej na wykonywalną, włączając proces uruchamiania i uzyskiwania wartości wyrażeń.
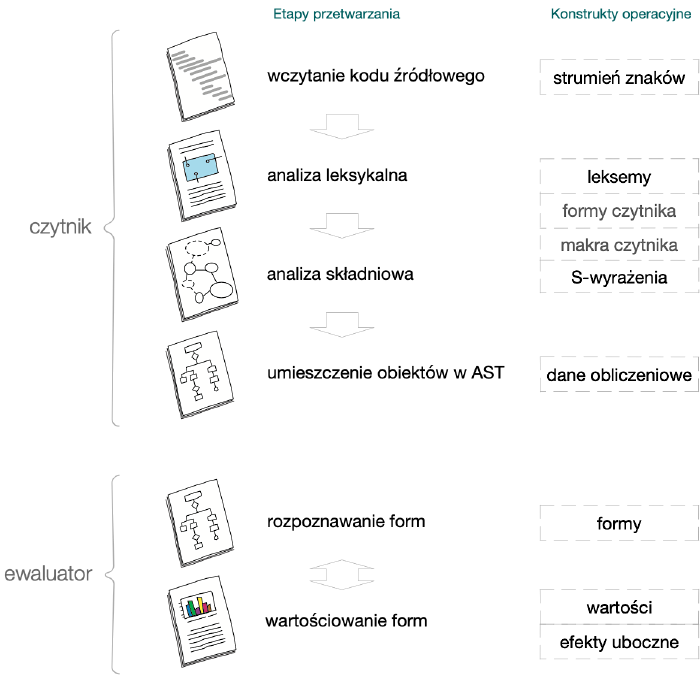
Pytania i odpowiedzi
Odpowiedzmy sobie na kilka pytań, które pozwolą podsumować wprowadzenie do podstawowych mechanizmów obecnych w Lispach (i w Clojure):
-
Jaka jest różnica między S-wyrażeniem a listą?
S-wyrażenie to gramatyczny element składni – symboliczny sposób organizowania kodu źródłowego w pliku tekstowym. Z kolei lista to umieszczana w pamięci struktura danych, która pozwala przechowywać dane w postaci zagnieżdżonej, zachowując informacje o kolejności ich występowania. Lista jest dobrym sposobem reprezentowania obiektów zdefiniowanych listowymi S-wyrażeniami z uwagi na podobieństwo aranżacji. W dialektach języka Lisp listy są używane do przechowywania danych w abstrakcyjnym drzewie składniowym, ale można z nich także korzystać w programach do operowania na danych użytkowych.
-
Jaka jest różnica między S-wyrażeniem a atomem?
Atom też jest S-wyrażeniem, lecz niezłożonym. W abstrakcyjnym drzewie składniowym nie będzie reprezentowany obiektem listy, a w postaci tekstowej programu nie wyrazimy go elementami umieszczonymi w nawiasach.
-
Jaka jest różnica między S-wyrażeniem a formą?
Forma to poprawne składniowo S-wyrażenie wczytane do pamięci i przekształcone do postaci znanych struktur danych, które jest gotowe do wartościowania (obliczania jego wartości w procesie ewaluacji).
-
Jaka jest różnica między symbolem a zmienną globalną?
Zmienna globalna to umieszczony w mapie zwanej przestrzenią nazw obiekt typu
Var, który przechowuje odwołanie do innego obiektu (wartości). Symbol to obiekt typuSymbol, który nie przechowuje żadnego odwołania, ale w tej samej mapie używany jest do identyfikowania obiektu typuVar(jest kluczem indeksującym). Można powiedzieć, że symbol nazywa zmienną globalną.
Zobacz także:

