Rozwiązania niektórych problemów obliczeniowych mogą być czytelnie wyrażone w postaci rekurencyjnej lub zapętlonej. W Clojure istnieją konstrukcje, które pozwalają implementować algorytmy w taki właśnie sposób.

Pętle i rekurencja

Algorytmy, w których występuje konieczność przeliczania pewnego wyrażenia lub zestawu wyrażeń więcej niż raz, mogą być w Clojure zaprogramowane z użyciem dwóch mechanizmów: pętli lub rekurencji.

W paradygmacie funkcyjnym unika się typowych zapętleń, chociaż niektóre problemy można łatwiej wyrażać i wydajniej rozwiązywać stosując podejście strukturalne, z którego pętle się wywodzą. Clojure daje więc wolną rękę programiście i obsługuje niektóre z ich rodzajów. Z kolei rekurencja pozwala w czytelny sposób definiować funkcje, których działanie wymaga powtórzonego wykonania większości operacji wchodzących w skład ich ciał. Można więc powiedzieć, że pętle i rekurencja służą do wyrażania rozwiązań problemów, które przedstawione w inny sposób byłyby mniej spójne i na przykład zawierały powtórzone czy nazbyt zagnieżdżone fragmenty kodu.

Uwaga: Stosowanie pętli i rekurencji w celu przetwarzania wieloelementowych kolekcji jest często nadużywane. Zawsze warto zbadać, czy dany problem może być rozwiązany z wykorzystaniem dostępu sekwencyjnego i funkcyjnych mechanizmów przekształcania (kaskadowego filtrowania, odwzorowywania i redukowania zbiorów danych).

Pętle

Pętla (ang. loop) to konstrukcja, która pozwala na wielokrotne powtarzanie tych samych obliczeń w odniesieniu podanego wyrażenia lub zestawu wyrażeń z możliwym wielokrotnym wywoływaniem efektów ubocznych. Przeliczanie wiąże się oczywiście z uruchamianiem związanych z wyrażeniami podprogramów. Z funkcyjnego punktu widzenia pętle można uznać za ograniczoną formę rekurencji, a dokładniej tzw. rekurencji ogonowej.

W językach programowania bazujących na paradygmacie imperatywnym i strukturalnym wewnątrz pętli może pojawić się konstrukcja sterująca, która pozwala na wykonanie skoku do pierwszej instrukcji lub wyjście z pętli. W językach funkcyjnych i akcentujących paradygmat funkcyjny możemy mieć kłopot ze znalezieniem odpowiedników tego typu konstrukcji, ponieważ pętle są tam przede wszystkim specyficznymi wyrażeniami, tzn. dokonują wielokrotnego wartościowania podanych form, ale nie umożliwiają niskopoziomowego sterowania wykonywaniem się podprogramu (np. wspomnianych skoków czy wyjść). W Lispach, a więc i w Clojure, aby osiągać podobne efekty korzysta się z odpowiedników pętli i z wyrażeń warunkowych.

Pewnym wyjątkiem od powyższego jest w Clojure forma recur, która zostanie omówiona później. Pozwala ona wykonać skok do ustanowionego wcześniej miejsca początkowego pętli z opcjonalną zmianą powiązań leksykalnych podanych symboli z wartościami.

Wyróżniamy następujące rodzaje pętli:

• pętle warunkowe,
• pętle kolekcyjne,
• pętle ogólne,
• pętle licznikowe,
• pętle powtórzeniowe,
• pętle nieskończone.

Pętle warunkowe

Pętla warunkowa (ang. condition-controlled loop) to taka pętla, dla której określono warunek zakończenia przetwarzania. Warunek ten jest sprawdzany po każdorazowym przeliczeniu wartości wyrażeń umieszczonych w ciele pętli lub przed wykonaniem wartościowania.

Pętla warunkowa, while

Makro while służy do tworzenia pętli warunkowych. Przyjmuje ono jeden obowiązkowy argument, którym powinno być wyrażenie warunkowe. Każdy następny argument będzie potraktowany jako wyrażenie wchodzące w skład ciała pętli i będzie przeliczane dopóty, dopóki podany warunek jest spełniony. Za spełnienie warunku uznaje się sytuację, w której podane wyrażenie zwraca wartość różną od nil i różną od false. Testowanie warunku odbywa się przed wartościowaniem wyrażeń.

Makro zwraca wartość nieustaloną nil.

Warto zauważyć, że pętla na bazie while będzie badała warunek, który związany jest ze zmiennymi dynamicznymi, zmiennymi lokalnymi, efektem ubocznym funkcji obsługującej wejście/wyjście, albo też z wartościami powiązanymi z globalnym stanem reprezentowanym jednym z typów referencyjnych. Dzieje się tak, ponieważ w konstrukcji tej nie mamy do czynienia z obsługą lokalnych powiązań, które wyrażałyby wartość obsługiwanego przez mechanizm pętli licznika bądź innej formy wyrażającej stan. Wartość używana do sprawdzania warunku musi więc pochodzić z zewnątrz.

Użycie:

• (while warunek & wyrażenie…).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

(with-local-vars [a 1 b 1]
  (while (< @a 8)
    (println @a)
    (var-set a (+ @a @b))
    (var-set b (inc @b))))
; >> 1
; >> 2
; >> 4
; >> 7
; => nil

Pętle kolekcyjne

Pętla kolekcyjna (ang. collection-controlled loop), zwana też pętlą typu foreach (ang. foreach loop), pozwala na wykonywanie pewnych wyrażeń dla każdego elementu podanej kolekcji lub innej wieloelementowej struktury.

W Clojure następcze przetwarzanie struktur w tym stylu można zrealizować korzystając z sekwencyjnego interfejsu dostępu i obsługujących sekwencje funkcji oraz makr, do których należą między innymi: doseq, doall, dorun, cycle, map i reduce.

Jeżeli mamy do czynienia ze strukturą danych, która pozwala na dostęp sekwencyjny i istnieje możliwość kaskadowego przetwarzania jej elementów w celu rozwiązania problemu, jest to zalecany sposób.

Pętle ogólne

Pętla ogólna (ang. generic loop), zwana też ogólnym dostępem następczym (ang. general iteration) pozwala uzyskiwać dostęp do kolejnych elementów wielu sekwencyjnych struktur danych jednocześnie, a umożliwia to zestaw wielu liczników powiązanych z ich pozycjami i warunków zakończenia przetwarzania. Przykładem takiej pętli jest znana z języka C instrukcja for.

Pętla ogólna, for

W Clojure pętlę ogólną możemy utworzyć z wykorzystaniem makra for i zestawów danych wyposażonych w sekwencyjne interfejsy dostępu. Jej zadanie polega na operowaniu na elementach powiązanych leksykalnie z symbolami w wektorze powiązań, który trzeba podać jako pierwszy argument. Mogą w nim znaleźć się również tzw. modyfikatory o etykietach wyrażonych słowami kluczowymi:

• :let   (wywołujący let),
• :when  (wywołujący when),
• :while (wywołujący while).

Umieszczenie modyfikatora w wektorze powiązań sprawi, że będzie wywołana forma specjalna lub makro o odpowiadającej mu nazwie, a znajdujące się po nim wartości zostaną przekazane jako argumenty.

Rezultatem wywołania for jest sekwencja składająca się z wartości generowanych przez wyrażenie podane jako drugi argument. W wyrażeniu tym można korzystać z symboli powiązanych z wartościami w wektorze powiązań. W każdej iteracji powiązania będą aktualizowane, odnosząc się do kolejnych elementów sekwencji. W przypadku więcej niż jednej pary powiązaniowej makro for dokona zagnieżdżonej iteracji dla każdego elementu z każdym, poczynając od elementów pierwszego powiązania.

Użycie:

• (for wektor-powiązań wyrażenie).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

;; mnożenie przez 2
(for [element '(1 2 3)] (* element 2))
; => (2 4 6)

;; wykorzystanie modyfikatorów
(for [element '(1 2 3)
      :let    [razy-dwa (* element 2)]
      :while  (< razy-dwa 5)]
  razy-dwa)
; => (2 4)

;; tworzenie sekwencji wektorów z kombinacjami
;; (zagnieżdżone iteracje)
(for [liczba '(1 2 3)
      litera '(:a :b)]
  [litera liczba])
; => ([:a 1] [:b 1] [:a 2] [:b 2] [:a 3] [:b 3])

Zobacz także:

• „Zaawansowane przekształcanie”, rozdział X.

Pętle licznikowe

Pętla licznikowa (ang. count-controlled loop), zwana też pętlą iteracyjną to pętla, która po każdym przebiegu dokonuje modyfikacji podanego licznika lub liczników. Pętla kończy pracę, gdy spełniony zostanie warunek zakończenia związany z bieżącą wartością licznika (np. gdy będzie on równy zeru lub innej, podanej wartości). W pętli tego typu warunek zakończenia i początkowa wartość licznika muszą być znane zanim rozpocznie się jej praca.

W wyrażeniach umieszczanych w pętli można korzystać z wartości licznika, na przykład do wskazywania elementu uporządkowanej kolekcji o podanym numerze indeksu.

W Clojure nie istnieje konstrukcja specyficzna dla pętli licznikowych, jednak można użyć na przykład makra for z sekwencją reprezentującą zakres liczbowy czy makra while.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

;; z licznikiem i warunkiem określonym wartością końcową
(for [n (range 4)] (println n))
; >> 0
; >> 1
; >> 2
; >> 3
; => (nil nil nil nil)

;; z licznikiem i warunkiem wyrażonym wprost
(for [n (range 4 10)
      :while (<= n 8)]
  (println n))
; >> 4
; >> 5
; >> 6
; >> 7
; >> 8
; => (nil nil nil nil nil)

Zauważmy, że w powyższych przykładach makro for poza efektami ubocznymi zwróciło sekwencje zawierające wartości generowane przez kolejne wywołania podanych wyrażeń (w naszym przypadku nil). Jeżeli jest to wysoce niepożądane, możemy:

• użyć funkcji dorun, która sprawi, że wartość zwracana przez makro for będzie zignorowana i zastąpiona pojedynczą wartością nil;

• skorzystać z innych konstrukcji, na przykład: doseq, loop czy while (wraz z with-local-vars).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

(dorun (for [n (range 4)] (println n)))
; >> 0
; >> 1
; >> 2
; >> 3
; => nil

(doseq [n (range 1 4)]
  (println n))
; >> 1
; >> 2
; >> 3
; => nil

(loop [n 3]
  (when (<= n 5)
    (println n)
    (recur (inc n))))
; >> 3
; >> 4
; >> 5
; => nil

(with-local-vars [n 5]
  (while (< @n 8)
    (println @n)
    (var-set n (inc @n))))
; >> 5
; >> 6
; >> 7
; => nil

Pętle powtórzeniowe

Pętla powtórzeniowa, zwana też pętlą typu times (ang. times loop), jest pętlą o określonej liczbie powtórzeń, lecz bez deklarowania wartości początkowej licznika i warunku zakończenia. Podczas użycia należy podać po prostu liczbę iteracji.

Pętla powtórzeniowa, dotimes

Makro dotimes pozwala utworzyć pętlę o określonej liczbie powtórzeń. Przyjmuje ono jeden obowiązkowy argument, którym powinien być uproszczony (nie zawierający konstrukcji dekompozycyjnych) wektor powiązań złożony z dokładnie jednej pary powiązaniowej: symbolu i liczby powtórzeń. Kolejne argumenty to wyrażenia stanowiące ciało pętli, w którym można korzystać z powiązanego wcześniej symbolu – dla każdego przebiegu powiązana z nim wartość będzie zmieniała się od 0 do wartości o jeden mniejszej, niż podana liczba powtórzeń.

Wartością zwracaną przez makro dotimes jest nil.

Użycie:

• (dotimes wektor-powiązań & wyrażenie…).

1
2
3
4
5

(dotimes [n 4] (println n))
; >> 0 
; >> 1
; >> 2
; >> 3

Pętle nieskończone

Pętla nieskończona (ang. infinite loop), zwana też pętlą nieograniczoną (ang. indefinite loop) jest taką pętlą, której liczba przebiegów nie jest określona, a więc potencjalnie może się ona wykonywać bez przerwy.

W Clojure nie istnieje konstrukcja typowa dla pętli nieskończonej, lecz można ją utworzyć, bazując na dostępnych formach specjalnych: loop i recur lub while.

1
2
3
4
5
6
7
8

;; użycie loop i recur
(loop []
  (println "w pętli")
  (recur))

;; użycie while
(while true
  (println "w pętli"))

Innym rozwiązaniem może być skorzystanie z funkcji obsługujących sekwencje:

• cycle, która generuje leniwą i potencjalnie nieskończoną sekwencję złożoną z cyklicznie powtarzanych elementów pochodzących z podanej kolekcji;

• repeat, która generuje leniwą i potencjalnie nieskończoną sekwencję złożoną z elementów o podanej wartości;

• repeatedly, która generuje leniwą i potencjalnie nieskończoną sekwencję dla rezultatów stanowiących kolejne wywołania przekazanej funkcji.

Rekurencja

Rekurencja (ang. recurrence), zwana też rekursją (ang. recursion) jest takim schematem postępowania w rozwiązywaniu problemu, w którym jeden z etapów polega na użyciu właśnie tego schematu.

Realizować następczo jest rzeczą ludzką, rekursywnie: boską.  
— L. Peter Deutsch

Obiekty uruchomieniowe, które działają w sposób rekurencyjny muszą mieć trzy podstawowe właściwości:

1. Powinny obsługiwać przynajmniej jeden przypadek bazowy (ang. base case), w którym rezultat generowany jest natychmiastowo, bez odwoływania się obiektu do samego siebie.

2. Powinny obsługiwać przynajmniej jeden przypadek rekursywny (ang. recursive case), gdzie następuje odwołanie się obiektu do samego siebie, aby uzyskać rezultat.

3. Powinny zawierać przynajmniej jeden warunek zakończenia rekurencji, który prowadzi do skrócenia (redukcji) rezultatów, dążąc do przypadku bazowego.

Przypadek bazowy nazywa się czasem przypadkiem prostym, a warunek zakończenia rekurencji warunkiem zatrzymania.

Tworząc implementacje rekurencyjnych algorytmów, należy odpowiedzieć na następujące pytania:

• Jakie są warunki przypadku bazowego?

• Jakie są warunki przypadku rekursywnego?

• Jaki jest sposób redukcji problemu, który przypadki rekursywne sprowadzi do przypadków bazowych?

Może również zdarzyć się tak, że dany problem nie jest problemem funkcyjnym i próba rozwiązania go rekurencyjnie będzie nieoptymalna pod względem czasowej bądź pamięciowej złożoności obliczeniowej. W takich przypadkach lepiej skorzystać z pętli czy nawet konstrukcji w stylu imperatywnym (np. z wykorzystaniem lokalnych obiektów typu Var).

Istnieje kilka rodzajów rekurencji, które różnią się sposobem wywoływania podprogramu własnego i mechanizmem przekazywania wartości. W Clojure możemy obsługiwać następujące:

• rekurencja zwykła (z użyciem wywołań funkcji w nich samych),
• rekurencja ogonowa (z użyciem konstrukcji recur),
• rekurencja wzajemna (z użyciem funkcji trampoline),
• rekurencja zagnieżdżona (z użyciem wywołań funkcji lub recur).

Higieniczny programista – przykład

Aby zrozumieć rekurencję,
musisz najpierw zrozumieć rekurencję.  
— D. Hunter

Spróbujmy zastanowić się nad hipotetycznym przypadkiem programisty, który dba o higienę. W tym celu każdego ranka udaje się pod prysznic, gdzie korzysta z szamponu, aby umyć włosy. Jakie instrukcje należałoby umieścić na etykiecie specyfiku, aby proces przebiegał pomyślnie?

Mogłoby to wyglądać w ten sposób:

1. Otworzyć butelkę.
2. Nanieść niewielką ilość na włosy.
3. Zamknąć butelkę.
4. Spłukać.
5. Czynność powtórzyć.

W krążącym w Sieci dowcipie o informatyku, który w ten sposób myje włosy, znajdujemy naszego bohatera martwego z wycieńczenia, ponieważ brakuje warunku zakończenia rekurencji i dochodzi do nieskończonego zapętlenia procesu. Rzeczywistość nie byłaby jednak tak tragicznie zabawna, ponieważ podobnie jak w pamięci komputera, tu również mamy do czynienia ze skończonymi zasobami. Po prostu wystąpiłaby sytuacja wyjątkowa, gdy po kilkunastu czy kilkudziesięciu powtórzeniach skończyłby się szampon.

Jak więc mogłaby wyglądać rekursywna instrukcja, którą zrozumiałby nasz higieniczny koder? Spróbujmy:

1. Otworzyć butelkę.
2. Nanieść niewielką ilość na włosy.
3. Zamknąć butelkę.
4. Spłukać.
5. Jeżeli włosy są brudne: czynność powtórzyć.

W ostatnim punkcie mamy do czynienia z warunkiem zakończenia rekurencji. Tym sposobem zadbaliśmy o drogocenny czas obliczeniowy naszego hipotetycznego czyścioszka!

Warto zauważyć, że zadania z punktów o numerach 2 i 4 mogą być w naszym przykładzie przypadkami bazowymi (właściwymi czynnościami wiodącymi do rozwiązania problemu), natomiast punkt nr 5 to przypadek rekursywny (prowadzący do powtórzenia wszystkich czynności).

Rekurencja nazwana i nienazwana

Czasem możemy spotkać się z nazwami rekurencja nazwana (ang. named recursion) i rekurencja nienazwana (ang. unnamed recursion), zwana też rekurencją anonimową (ang. anonymous recursion). Pierwszy termin oznacza, że rekurencyjne przeliczanie wyrażenia odbywa się z wykorzystaniem nadanej mu wcześniej nazwy, a drugi, że nie korzysta się z żadnego powiązania z identyfikatorem, lecz odwołuje do podprogramu w inny sposób, np. z użyciem specjalnych konstrukcji bądź przez przekazywanie obiektu funkcyjnego do funkcji wyższego rzędu.

W Clojure za rekurencję nazwaną można uznać wszelkie rekurencyjne wywołania funkcji z użyciem powiązanej z nią wcześniej symbolicznej nazwy. Z kolei za rekurencję nienazwaną:

• korzystanie z konstrukcji recur;
• używanie wywołań funkcji sprzężonej (iterate);
• przekazywanie obiektu funkcyjnego w argumentach wywołania;
• używanie operatorów punktu stałego.

Warto zauważyć, że za rekurencję anonimową uznamy nawet wywołania funkcji nazwanej, jeżeli sposób rekursywnego odwoływania się do niej nie korzysta z nazwy, lecz np. z konstrukcji recur. Podobnie w przypadku rekurencji nazwanej: możemy uznać, że nawet wywołania funkcji anonimowej, jeżeli korzystają z jej symbolicznego identyfikatora (podanego na początku definicji, tuż po symbolu fn), są formą rekurencji nazwanej.

Rekurencja nieogonowa

Rekurencja nieogonowa (ang. non-tail recursion), zwana czasem rekurencją zwykłą (ang. plain recursion) lub po prostu rekurencją, polega na wywoływaniu podprogramu realizującego pewne zadanie przez samego siebie. W Clojure rekurencyjnych wywołań możemy dokonywać z wyrażenia umieszczonego w ciele funkcji.

Dzięki zastosowaniu rekurencji zwykłej jesteśmy w stanie w przejrzysty i funkcyjny sposób wyrażać sposoby rozwiązywania wielu problemów. Należy jednak być ostrożnym, ponieważ w Clojure nie mamy do czynienia z automatyczną optymalizacją rekurencji, co może prowadzić do przepełnienia stosu wywołań (ang. call stack). Wynika to ze sposobu, w jaki odbywa się wywoływanie funkcji. Programy komputerowe korzystają ze stosu, aby umieszczać na nim informacje o aktualnie realizowanych podprogramach (np. wywołanych funkcjach). Powodem korzystania z takiej struktury jest konieczność powrotu z podprogramu i przekazania sterowania do instrukcji następującej zaraz po miejscu jego wywołania.

Stos wywołań złożony jest z tzw. ramek stosu (ang. stack frames). Każde odwołanie się do kodu funkcji przez jej podprogram sprawia, że na stosie pojawia się nowa ramka. Jeżeli funkcja wywołuje samą siebie (własny podprogram) wielokrotnie, to na stosie umieszczanych jest odpowiednio dużo ramek. Każda z nich będzie zajmowała określony obszar pamięci, której rozmiar jest ograniczony. Gdy wywołań będzie zbyt wiele, przestrzeni pamięciowej nie wystarczy i wykonywanie się programu zostanie awaryjnie przerwane.

Powyższe oznacza, że w praktyce powinniśmy stosować rekurencję nieogonową tylko tam, gdzie nie będziemy mieli do czynienia ze zbyt wieloma rekurencyjnymi wywołaniami. Jeżeli dany algorytm na to nie pozwala, należy zastosować inne, omówione niżej rodzaje rekurencji lub skorzystać z pętli.

Rekurencyjne wywoływanie funkcji

Oczywistym przykładem rekurencji nieogonowej jest wywołanie funkcji w wyrażeniu jej ciała. Może być to funkcja anonimowa lub nazwana. Wywołanie rekurencyjne w zapisie nie różni się od zwyczajnego wywołania funkcji: posługujmy się listowym S-wyrażeniem, którego pierwszym elementem jest symbol wskazujący na funkcję.

Spróbujmy zdefiniować funkcję o symbolicznej nazwie !, która będzie rekurencyjnie realizowała algorytm silni:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

(defn ! [n]
  (if (zero? n)           ; warunek zakończenia rekurencji
    1                     ; przypadek bazowy
    (*' (! (dec n)) n)))  ; przypadek rekursywny
                          ;  · wynik wywołania dla n-1 mnożony przez n
(! 1)   ; => 1
(! 5)   ; => 120
(! 21)  ; => 51090942171709440000N

(! 7000)
; >> #<StackOverflowError java.lang.StackOverflowError>

Zauważmy, że w linii nr 4 zamiast ze standardowego operatora mnożenia, korzystamy z operatora obsługującego potencjalnie duże liczby: *'. Dzięki niemu unikamy pojawiania się w linii nr 9 błędu związanego z przepełnieniem zakresu.

W ostatniej linii przykładu doszło do awaryjnego przerwania pracy i zgłoszenia wyjątku StackOverflowError komunikującego przepełnienie stosu. Przyczyną była zbyt duża liczba odłożonych na stos ramek. Wywołując funkcję, przekazaliśmy jej jako argument liczbę 7000, która w naszym przypadku oznacza dążenie do siedmiu tysięcy zagnieżdżonych wywołań. Receptą na to jest skorzystanie na przykład z rekurencji ogonowej.

Operator paradoksalny Y: Y-combinator

Operator punktu stałego (ang. fixed-point combinator) jest taką funkcją wyższego rzędu, która dla podanej w argumencie funkcji zwraca jej punkt stały, czyli miejsce, w którym zwracana wartość jest tożsama z przekazanym argumentem.

Popularnym operatorem punktu stałego jest pochodzący z rachunku lambda operator paradoksalny Y (ang. Y-combinator). Jego nazwa pochodzi od tzw. paradoksu Curry’ego, w którym zdanie logiczne definiuje własną prawdziwość, np.: Jeżeli to zdanie jest prawdziwe, Lisp jest najmocniejszym językiem programowania.

Ponieważ operator Y daje się wyrazić w rachunku lambda, więc – jak nietrudno się domyślić – możemy zaimplementować go w Lispach, a więc i w Clojure. Do czego można go użyć? Okazuje się, że dzięki niemu możliwe jest wyrażanie rekurencyjnych funkcji, które nie będą wprost odwoływały się do samych siebie (np. z użyciem symbolicznych nazw). Oznacza to, że z użyciem operatora Y możemy wyrazić prostą rekurencję anonimową przez przekazywanie bieżącej funkcji jako argumentu.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

;; operator Y
(defn Y [f]
  (#(% %)
   #(f (fn [& args] (apply (% %) args)))))

;; silnia 
(defn ! [f] #(if (zero? %) 1 (*' % (f (dec %)))))

;; wywołania
((Y !) 0)   ; => 1
((Y !) 1)   ; => 1
((Y !) 2)   ; => 2
((Y !) 12)  ; => 479001600

Zauważmy, że ta implementacja operatora punktu stałego Y nie jest zoptymalizowana i przy głębszych poziomach rekurencji dochodzić będzie do przepełnienia stosu.

Rekurencja ogonowa

Rekurencja ogonowa (ang. tail recursion) – zwana też rekurencją prawostronną (ang. right recursion), wywołaniem ogonowym (ang. tail call) lub rekurencją końcową – jest rodzajem rekurencji, w którym najpierw przeprowadzane są wszelkie możliwe obliczenia, a dopiero potem następuje wywołanie rekursywne. Istotne jest to, aby wywołanie to było ostatnim przeliczanym wyrażeniem ciała funkcji lub funkcyjnej konstrukcji.

Dzięki powyższemu kompilatory są w stanie przeprowadzać tzw. optymalizację wywołania ogonowego (ang. tail-call optimization, skr. TCO) i nie tworzyć nowych ramek odkładanych na stosie, bo każde kolejne wywołanie funkcji zastępuje wywołanie poprzedniej (korzysta z jej ramki). Jest to możliwe, ponieważ wywołanie to jest ostatnim wyrażeniem i po jego wartościowaniu nie ma już potrzeby wracać do konkretnego miejsca w podprogramie, a więc i pamiętać miejsca tego powrotu na stosie.

W Clojure nie mamy do czynienia z automatycznym wykrywaniem wywołań ogonowych, ani tym bardziej z automatycznym przekształcaniem kodu źródłowego w taki sposób, aby wywołania nieogonowe transformować do bardziej iteracyjnej postaci. Rekurencję ogonową należy więc wyrazić wprost, z użyciem konstrukcji recur.

Ogonowa rekurencja anonimowa, recur

Forma specjalna recur pozwala tworzyć ogonowe wywołania podprogramów, które nie powodują odkładania ramek na stos. Jej działanie polega na przeniesieniu wykonywania podprogramu do określonego wcześniej punktu początkowego, który powinien być zdefiniowany w obejmującym wywołanie recur kontekście leksykalnym.

Forma recur przyjmuje zero lub więcej wyrażeń inicjujących, których wartości zostaną przekazane do konstrukcji stanowiącej wspomniany punkt początkowy. W przypadku funkcji będą to jej argumenty, a w przypadku formy specjalnej loop wyrażenia inicjujące. W ten sposób zaktualizowane zostaną powiązania obejmującej formy – ich symbole (reprezentujące parametry funkcji lub leksykalne powiązania konstrukcji loop) będą odnosiły się do nowych wartości.

W przypadku funkcji wieloczłonowych punktem początkowym będzie bieżące ciało (przypisane do danej argumentowości), a nie cała funkcja.

Użycie:

• (recur & wyrażenie-inicjujące…).

Następujące konstrukcje mogą być zastosowane jako punkty początkowe recur:

• funkcje anonimowe – formy fn i letfn,
• funkcje nazwane – makro defn,
• forma specjalna loop.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

;; funkcje anonimowe
((fn !                               ; wywołanie funkcji anonimowej
   ([n] (! n 1))                     ; pierwsze ciało: wywołanie drugiego
   ([n acc]                          ; drugie ciało:
    (if (zero? n)                    ;  · warunek zakończenia rekurencji
      acc                            ;    · przypadek bazowy
      (recur (dec n) (*' acc n)))))  ;    · przypadek rekursywny
 12)                                 ; argument wywołania funkcji
; => 479001600

;; funkcje nazwane
(defn !                              ; definicja funkcji
  ([n] (! n 1))                      ; pierwsze ciało: wywołanie drugiego
  ([n acc]                           ; drugie ciało:
    (if (zero? n)                    ;  · warunek zakończenia rekurencji
      acc                            ;    · przypadek bazowy
      (recur (dec n) (*' acc n)))))  ;    · przypadek rekursywny
                                     ; 
(! 12)                               ; wywołanie funkcji nazwanej
; => 479001600

;; forma specjalna loop
(loop [n 12 acc 1]                   ; wywołanie formy specjalnej loop
  (if (zero? n)                      ;  · warunek zakończenia rekurencji
    acc                              ;    · przypadek bazowy
    (recur (dec n) (*' acc n))))     ;    · przypadek rekursywny
; => 479001600

Punkt początkowy, loop

Makro loop pozwala na ustalenie innego niż początkowe wyrażenie ciała funkcji punktu początkowego rekurencji ogonowej z możliwością tworzenia powiązań leksykalnych. Powiązania te mogą być następnie aktualizowane przez wywoływanie recur. Dzięki loop możliwe jest budowanie anonimowych, rekurencyjnie wykonywanych podprogramów, które oszczędzają przestrzeń stosu.

Użycie:

• (loop wektor-powiązań & wyrażenie…).

Pierwszym przekazywanym argumentem powinien być wektor powiązań, w którym dokonać możemy początkowego przypisania wartości do symbolicznych nazw (z możliwą dekompozycją). Kolejne, opcjonalne argumenty to wyrażenia stanowiące ciało konstrukcji. Będą one wartościowane za każdym jej wywołaniem, a w ich zasięgu leksykalnym można używać symboli powiązanych z wartościami w podanym wcześniej wektorze.

Ostatnimi wyrażeniami w ciele konstrukcji loop (pod względem poziomu zagłębienia w drzewie składniowym) mogą być wspomniane wcześniej wywołania recur. Ich obecność sprawi, że przetwarzanie wszystkich wyrażeń wewnątrz loop zacznie się od początku.

Jako argumenty przekazywane do recur należy podać nowe wartości symboli obecnych w (podanym jako pierwszy argument) wektorze powiązań. Umieszczać należy wyłącznie wartości (odpowiedniki wyrażeń inicjujących lub argumentów pozycyjnych), a nie całe pary powiązaniowe.

Wartością zwracaną przez loop jest wartość ostatnio obliczonego wyrażenia lub wartość nil, jeżeli żadne wyrażenie nie zostało obliczone w ostatnim przebiegu.

1
2
3
4
5

(loop [n 12 acc 1]                ; wywołanie formy specjalnej loop
  (if (zero? n)                   ;  · warunek zakończenia rekurencji
    acc                           ;    · przypadek bazowy
    (recur (dec n) (*' acc n))))  ;    · przypadek rekursywny
; => 479001600

Powyższy przykład z loop jest po prostu bardziej wydajnym odpowiednikiem następującego:

1
2
3
4
5
6

((fn [n acc]                      ; wywołanie funkcji anonimowej
  (if (zero? n)                   ;  · warunek zakończenia rekurencji
    acc                           ;    · przypadek bazowy
    (recur (dec n) (*' acc n))))  ;    · przypadek rekursywny
 12 1)                            ; argumenty wywołania funkcji
; => 479001600

Który z kolei możemy zapisać w postaci nieogonowej:

1
2
3
4
5
6

((fn ! [n acc]                    ; wywołanie funkcji anonimowej
  (if (zero? n)                   ;  · warunek zakończenia rekurencji
    acc                           ;    · przypadek bazowy
    (! (dec n) (*' acc n))))      ;    · przypadek rekursywny
 12 1)                            ; argumenty wywołania funkcji
; => 479001600

Rekurencja zagnieżdżona

Rekurencja zagnieżdżona (ang. nested recursion) to specyficzny rodzaj rekurencji, w którym dochodzi do odwołania się obiektu do samego siebie przez przekazanie jego dodatkowej instancji w argumencie wywołania.

Dobrym przykładem rekurencji zagnieżdżonej jest funkcja Ackermanna, która jest funkcją rekurencyjną, ale nie pierwotnie rekurencyjną:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

(defn acker [m n]                 ; definicja funkcji
  (cond                           ; warunki zakończenia rekurencji
    (zero? m) (inc n)             ; przypadek bazowy
    (zero? n) (acker (dec m) 1)   ; przypadek rekursywny (r. pierwotna)
    :else     (acker              ; przypadek rekursywny (r. zagnieżdżona)
               (dec m)
               (acker m (dec n)))))

(acker 0  0)  ; => 1
(acker 1  0)  ; => 2
(acker 1  1)  ; => 3
(acker 2  2)  ; => 7
(acker 3 10)
; >> #<StackOverflowError java.lang.StackOverflowError>

Z uwagi na bardzo szybki przyrost liczby wywołań użycie funkcji z powyższego przykładu szybko kończy się przepełnieniem stosu. Receptą na to może być przekształcenie algorytmu w taki sposób, aby korzystał z rekurencji ogonowej:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

(defn acker [x y]                      ; definicja funkcji
  (loop [m x                           ; parametr m
         n y                           ; parametr n
         stos ()]                      ; lista akumulująca rezultaty
    (cond                              ; warunki zakończenia rekurencji
      (zero? m) (if (empty? stos)
                  (inc n)              ; przypadek bazowy
                  (recur (peek stos)   ; przypadek rekursywny
                         (inc n)
                         (pop stos)))
      (zero? n) (recur (dec m)         ; przypadek rekursywny
                       1
                       stos)
      :else     (recur m               ; przypadek rekursywny
                       (dec n)
                       (conj stos (dec m))))))

(acker 0  0)  ; => 1
(acker 1  0)  ; => 2
(acker 1  1)  ; => 3
(acker 2  2)  ; => 7
(acker 3 10)  ; => 8189

Zastosowaliśmy tu dodatkowy, trzeci argument, którego zadaniem jest przekazywanie rezultatów wywołań, które odzwierciedlają zmiany jednego z parametrów (m). Technika ta pozwala utworzyć własny wariant stosu dla pewnych danych, który może zajmować większy obszar pamięciowy, aby akumulować rezultaty pośrednie. W tym konkretnym przypadku własny stos pozwala składować efekty pracy dodatkowego wywołania, które w wersji nieogonowej jest zagnieżdżone.

Rekurencja pośrednia i wzajemna

Rekurencja pośrednia (ang. indirect recursion) to taki rodzaj rekurencji, w którym nie dochodzi do bezpośredniego odwołania się obiektu do samego siebie, lecz do odwołania do innego obiektu, który następnie korzysta z bieżącego.

Popularnym wariantem rekurencji pośredniej jest tzw. rekurencja wzajemna (ang. mutual recursion), gdzie kilka różnych obiektów naprzemiennie odwołuje się do siebie, aby realizować pewien algorytm.

Rekurencja wzajemna wywołań

Przykładem wzajemnej rekurencji mogą być naprzemienne wywołania dwóch lub większej liczby funkcji, np. w implementacji predykatów testujących parzystość i nieparzystość:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

(declare parzysta?)          ; deklaracja funkcji definiowanej później

(defn nieparzysta? [x]
  (and                       ; warunek zakończenia rekurencji
   (not= 0 x)                ; przypadek bazowy (gdy x równe 0)
   (parzysta? (dec x))))     ; przypadek rekursywny

(defn parzysta? [x]
  (or                        ; warunek zakończenia rekurencji
   (zero? x)                 ; przypadek bazowy (gdy x równe 0)
   (nieparzysta? (dec x))))  ; przypadek rekursywny

(nieparzysta? 0)  ; => false
(nieparzysta? 1)  ; => true
(nieparzysta? 2)  ; => false
(parzysta?    0)  ; => true
(parzysta?    1)  ; => false
(parzysta?    2)  ; => true

(nieparzysta? 2000000N)
; >> #<StackOverflowError java.lang.StackOverflowError>

W powyższym przykładzie funkcja nieparzysta? w przypadku rekursywnym dokonuje wywołania funkcji parzysta? dla podanego argumentu pomniejszonego o 1. Z kolei funkcja parzysta? robi to samo wywołując funkcję parzysta?. W efekcie będziemy mieli do czynienia z szeregiem wartości, z których każda jest o 1 mniejsza od pozostałych.

Tak będzie wyglądał stos wywołań dla (parzysta? 4):

1
2
3
4
5
6

(parzysta? 4)
  (nieparzysta? 3)
    (parzysta? 2)
      (nieparzysta? 1)
        (parzysta? 0)
          true

A tak dla (nieparzysta? 4):

1
2
3
4
5
6

(nieparzysta? 4)
  (parzysta? 3)
    (nieparzysta? 2)
      (parzysta? 1)
        (nieparzysta? 0)
          false

Warto zauważyć, że mamy tu do czynienia z rekurencją, która prowadzić może do wyczerpania miejsca pamięci stosu.

Optymalizacja wzajemnej, trampoline

Funkcja trampoline jest pomocna w optymalizowaniu algorytmów, które bazują na rekurencji wzajemnej, ponieważ pomaga uniknąć zużycia całej dostępnej pamięci stosu. Warunkiem koniecznym jest jednak zdefiniowanie rekurencyjnie wywoływanych funkcji w taki sposób, aby zwracanymi przez nie wartościami były obiekty typu funkcyjnego, a dopiero one mogą zawierać rekurencyjne wywołania właściwych funkcji. Dzięki temu trampoline jest w stanie dokonywać redukcji rezultatów, korzystając z wewnętrznego akumulatora zamiast ze stosu.

Użycie:

• (trampoline funkcja & argumenty).

Funkcja jako pierwszy, obowiązkowy argument przyjmuje funkcję, która zamiast rekurencyjnie wywoływać inną funkcję powinna zwracać obiekt funkcyjny dokonujący tej operacji. Kolejne, opcjonalne argumenty przekazywane do trampoline zostaną przekazane do podanej jej funkcji.

Jeżeli przekazana funkcja zwróci obiekt inny niż funkcję, zostanie to potraktowane jako przypadek bazowy i zwrócona będzie wartość, a wywoływanie kolejnych odwołujących się wzajemnie funkcji zakończy się.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

(defn fn-parzysta? [n]
  (or
   (zero? n)
   #(fn-nieparzysta? (dec n))))

(defn fn-nieparzysta? [n]
  (and
   (not= 0 n)
   #(fn-parzysta? (dec n))))

(defn parzysta?    [n] (trampoline fn-parzysta?    n))
(defn nieparzysta? [n] (trampoline fn-nieparzysta? n))

(nieparzysta? 2000000N)
; => false

Stos wywołań dla (nieparzysta? 3) przedstawia się tu następująco:

1
2
3
4
5
6
7

(nieparzysta? 3)
  (trampoline fn-nieparzysta? 3)
    (fn-nieparzysta? 3)
    (fn-parzysta? 2)
    (fn-nieparzysta? 1)
    (fn-parzysta? 0)
      true

Dzięki zastosowaniu funkcji trampoline uniknęliśmy odkładania na stos ramek zawierających adresy powrotne. Było to możliwe, ponieważ funkcja ta wywołuje każdy zwrócony obiekt funkcyjny, działając jak reduktor. Warunkiem jest oczywiście to, żeby przypadki rekursywne były obsługiwane przez zwracanie obiektów funkcyjnych, a nie bezpośrednie wywoływanie funkcji.

Ostatni przykład możemy uprościć, korzystając z konstrukcji letfn, aby nie tworzyć publicznie dostępnych funkcji:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

(defn parzysta? [n]
  (letfn [(parzyste [x]
            (or
             (zero? x)
             #(nieparzyste (dec x))))
          (nieparzyste [x]
            (and
             (not= 0 x)
             #(parzyste (dec x))))]
    (trampoline parzyste n)))

(defn nieparzysta? [n] (not (parzysta? n)))

(nieparzysta? 2000000N)
; => false

Spójrzmy jeszcze na użycie trampoline w odniesieniu do implementacji silni:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

(defn ! [n]
  (letfn
      [(n-liczba [koniec nr poprzednia]     ; generuje kolejną wartość
         (let [następna (*' n poprzednia)]
           (if (= koniec nr)                ; warunek zakończenia
             następna                       ;   · przypadek bazowy
             #(n-nr koniec nr następna))))  ;   · przypadek rekurencyjny

       (n-nr [koniec p-nr bieżąca]          ; generuje kolejny element
         #(n-liczba koniec (inc p-nr) bieżąca))]
    
    (trampoline n-liczba (if (zero? n) 1 n) 1 1)))

(! 1)     ; => 1
(! 2)     ; => 2
(! 21)    ; => 51090942171709440000N
(! 7000)  ; => 884200795…000N

Leniwe sekwencje

Leniwe sekwencje mogą być przykładem praktycznego wykorzystania rekurencji pośredniej, gdy funkcja generująca elementy odwołuje się do siebie przez wywoływanie odpowiednich funkcji pośredniczących.

Warto zaznaczyć, że często będziemy mieć tu do czynienia z zewnętrznym warunkiem zakończenia rekurencji (w formie funkcji wyższego rzędu, np. pobierającej tylko podany zakres elementów).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

(defn !
  ([n v]
   (let [nowa-n (inc n)
         nowa-v (*' n v)]
     (cons v (lazy-seq (! nowa-n nowa-v)))))
  ([n]
   (let [jeden (if (zero? n) 1 (/ n n))]
     (nth (! jeden jeden) n))))

(def s-silni (! 1 1))

(time (do (nth s-silni 1)     nil))  ; >> "Elapsed time: 0.082552 msecs"
(time (do (nth s-silni 20000) nil))  ; >> "Elapsed time: 1825.722463 msecs"
(time (do (nth s-silni 20000) nil))  ; >> "Elapsed time: 5.520258 msecs"
(time (do (nth s-silni 20001) nil))  ; >> "Elapsed time: 6.744783 msecs"
(time (do (nth s-silni 19999) nil))  ; >> "Elapsed time: 5.420101 msecs"

(! 1)     ; => 1
(! 2)     ; => 2
(! 21)    ; => 51090942171709440000N
(! 7000)  ; => 884200795…000N

W powyższym przykładzie mamy do czynienia z funkcją wieloczłonową o symbolicznej nazwie !, która w pierwszym wariancie przyjmuje dwa argumenty (parametry n i v), a w drugim jeden argument (parametr n). Pierwszy wariant zwraca leniwą sekwencję kolejnych rozwinięć silni i jest funkcją rekurencyjną, natomiast drugi służy do pobierania konkretnego elementu tej sekwencji, czyli obliczania wartości silni dla podanej wartości argumentu.

Argumenty n i v wariantu rekurencyjnego są początkowo równe 1. Jest to przypadek bazowy. Następnie przeprowadzane są obliczenia, które generują dwie nowe wartości na bazie tych argumentów. W pierwszym wywołaniu rezultatami będą liczby 2 i 1. Druga z wartości (1) zostanie wpisana do pierwszego slotu obiektu typu Cons, której slot drugi będzie odnosił się do leniwej sekwencji, której funkcją generującą będzie rekurencyjne wywołanie ! z argumentami 2 i 1. Przy kolejnym rekurencyjnym wywołaniu będzie to 3 i 2, a przy następnym 4 i 6. Wygenerowane z leniwej sekwencji komórki cons dla pierwszych 4 elementów będą więc miały następujące zawartości:

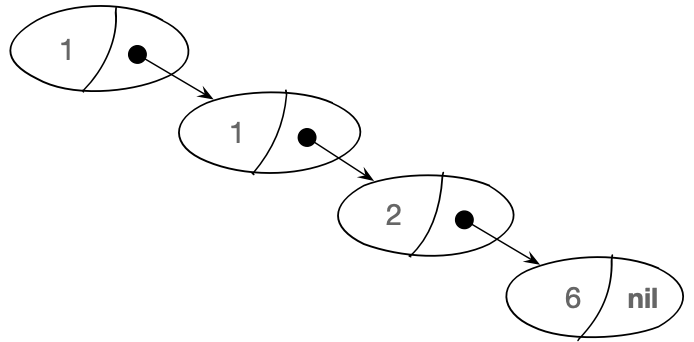
W przykładzie możemy też zauważyć, że rekurencyjne wywołanie funkcji jest zawarte w ciele makra lazy-seq. Działa ono w ten sposób, że dla podanych wyrażeń zwraca obiekt typu LazySeq, który sprawi, że ich wartości zostaną obliczone tylko przy pierwszym odwołaniu do zwracanego obiektu, a rezultaty zostaną wewnętrznie spamiętane. Każde kolejne odwołanie do wynikowej sekwencji będzie już korzystało z wcześniej obliczonych wartości.

Spamiętywanie

Rekurencja ogonowa i zwracanie obiektów funkcyjnych w przypadkach rekursywnych nie są jedynymi sposobami optymalizacji rekurencyjnych algorytmów. Jeżeli danych nie jest zbyt wiele, możemy posłużyć się tzw. spamiętywaniem (ang. memoization). Proces ten polega na zapisywaniu wartości zwracanych przez funkcje, aby przy kolejnych ich wywołaniach korzystać z już obliczonych rezultatów. Bazą, w której przechowywane są wyniki, jest zazwyczaj asocjacyjna struktura danych (np. mapa), której kluczami są przyjmowane argumenty, chociaż możliwe jest też tworzenie bardziej (lub mniej) skomplikowanych buforów.

W Clojure możemy spamiętywanie zaimplementować samodzielnie, albo skorzystać z funkcji memoize:

1
2
3
4
5
6
7
8
9

(defn !
  ([n] (! n 1))
  ([n acc] (if (zero? n) acc (recur (dec n) (*' acc n)))))

(def ! (memoize !))

(time (do (! 8000) nil))  ; >> "Elapsed time: 257.792908 msecs"
(time (do (! 8000) nil))  ; >> "Elapsed time: 0.0836 msecs"     (zapamiętany rezultat)
(time (do (! 7999) nil))  ; >> "Elapsed time: 294.067773 msecs"

Zauważmy, że w powyższym przykładzie nie mamy do czynienia z wykorzystaniem rezultatów pośrednich rekurencyjnych wywołań. W siódmej linii przykładu obliczyliśmy rozwinięcia ciągu rezultatów funkcji silnia dla wartości 8000, lecz mimo to w linii ostatniej (dla 7999) obliczenia przeprowadzane są ponownie. Zapamiętany został tylko konkretny wynik.

Aby było inaczej, możemy zdefiniować własną funkcję buforującą, np. tak, jak to pokazano w sekcji poświęconej Atomom, albo wyrazić algorytm w postaci leniwej sekwencji.